I have this idea that there are some mathematicians in my fictional afterworld Flimsy who are bent on doing some extremely demanding mathematical computations. The chief among these guys is the ghost of Charles Howard Hinton, a quirky character whom I’ve blogged about before, an early advocate of higher dimensional geometry.
My idea is that Hinton, who now lives in the Earth-based region of the afterworld, is computing such outré mathematical objects that he’s had to borrow energy from the neighboring realms of the afterworld, that is from the ghosts of Solsol and the ghosts of Bulber. And now the Solsol and Bulber ghosts are tired of waiting for their payback, and they plan to do a repo on Hinton. They’re going to siphon every living soul off Earth so as to pay off Hinton’s energy debt.

This is, in part, my satirical take on what the quantitative analysts of Wall Street did to the economy in 2008. But overcomputing is also something that interests me on its own.
Over the years, I’ve noticed that certain kinds of computations are inexhaustibly greedy, and that by dialing up certain of their parameters to values that seem not all that big, you can get a computation whose demands would overwhelm the physical world.
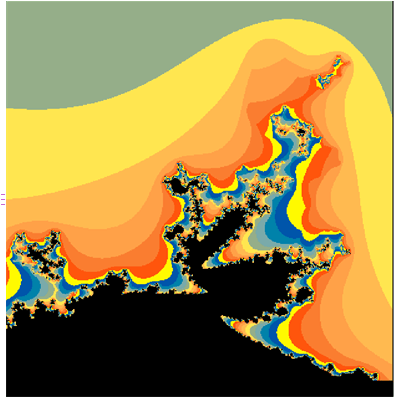
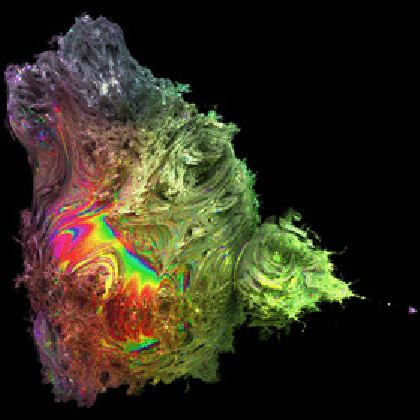
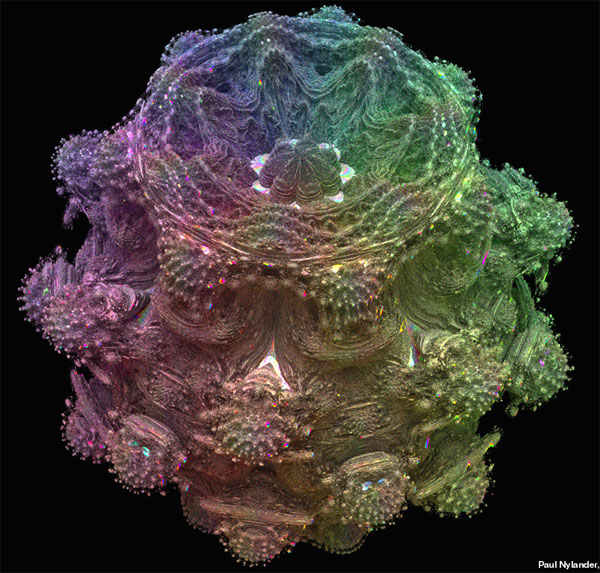
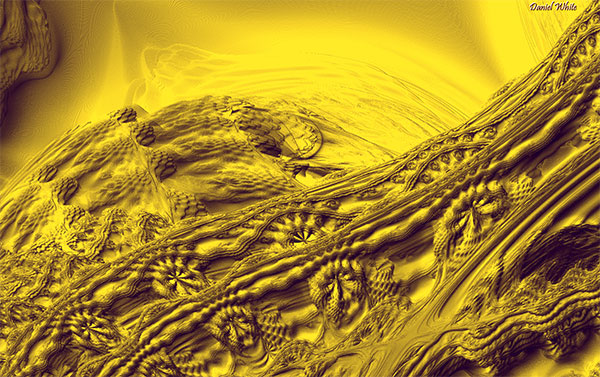
So what kind of computation is C. H. Hinton doing? Well, I’m going to have him computing a series of 3D fractal shapes that are based on a 27th-power polynomial equation, somewhat along the lines I described in my recent post “In Search of the Mandelbulb”
Let’s back up a step to see how gnarly his computation needs to be. What is the computational capacity of ordinary physical space? According to quantum mechanics, the smallest meaningful length is the Planck length, which, in meters, is 1 divided by 10-to-the-35th power. So the smallest meaningful volume is tiny block that is one Planck length long on each edge, and which holds a volume that’s the cube of the Planck length, that is, 1 divided by 10-to-the-105th power cubic meters.
[Note that I corrected this post on Oct 10, 2009 to accord with a comment by Fabiuz, that you can find below. Before Fabiuz I’d omitted the cubing stage.]
And the shortest meaningful time is the Planck time, which is how long it takes a light ray to travel a distance of on Planck length. Measured in seconds, the Planck time clocks in at 1 divided by 10-to-the-43rd power.
So if we assume that we might master a eldritch quantum computational technique that lets us carry out one computational operation per Planck length per Planck time, we’d be able to blaze along at 10-to-the-148th power operations per second per cubic meter.
It might actually be that our physical space is in fact doing this everywhere and everywhen…effortlessly. Just keeping itself going.

Planet Earth has a volume in cubic meters of about 10-to-the-21st power, so if we throw all of the planet at a problem, we can compute some 10-to-the-169th-power operations per second.
We might round it up to call it ten to the two-hundredth power, which happens to be googol squared—googol is the mathematicians’ old friend, that is, 10 to the hundredth power. Googol-squared ops per second!
The diameter of our observable universe is currently estimated to be about 10-to-the-27th-power meters, so the whole universe has a volume on the order of 10-to-the-81st-power meters. And if you set all of that space to computing, you’ll rack up some 10-to-the-229th-power operations per second. Less than a googol cubed.
Using the whole universe as a computer doesn’t give you a very dramatic gain over just using Earth—the reason for this is that, relatively speaking, the jump from Planck length to Earth is in fact bigger than the jump from Earth to Universe.

Now let’s think of computations so greedy that they can swamp this level of computational capacity.
(1) Use a parallel computation which is spread out across a very large number of voxels, that is, small volume cells of idealized mathematical space. You can really increase the number of voxels by requiring that you can zoom down very deep into your views of the object.
(2) Have the basic step of your computation per voxel be somewhat demanding. Have it use a higher-order formula, and have it require the formula to be iterated a large number of times.
(3) Run a very large number of these computations at once because, we’ll suppose, you’re searching through a space of all possible formulae—hoping to find the best one.
(4) And, just to keep the demand flowing, suppose that you want to update the output reasonably fast, say at a hundred times per second, so as to create a nice smooth animation.

I’ve been thinking about three-dimensional fractals lately, so let’s suppose that’s the kind of computation we’ll use. I’ll want to look at a 3D fractal that’s twisting and changing in real time as some parameter is varied.
The familiar Mandelbrot set is based on a quadratic equation in a two-dimensional space. For our illustrations, suppose we’re interested in three-dimensional analogs of the Mandelbrot set. And, to make it funky, suppose that instead of just looking at quadratic equations, we’ll be looking at higher-degree equations as well, where the “degree” of an equation is the highest power used. A quadratic equation has degree 2, a cubic equation has degree 3 and so on.
If we pass to higher degrees, it’ll be convenient to write the degree in the form (N/2) for convenience. We’ll be using complex numbers as parameters, so that means that one of these equations has N parameters. And evaluating a polynomial of this form takes on the order of N-squared steps.
In order to really get greedy with the computations, once we specify the degree of the polynomial we’re using, we’ll want to be looking at all possible variations on the polynomial of this degree. It’s like we’d be searching for the gnarliest or the most beautiful fifth-degree three-dimensional analog of the Mandelbrot Set. And we’ll suppose that the search can be automated by doing a brute-force search and ranking the results according to some mathematical measure such as entropy.

So now let’s see how high the computational demand might run.
First of all, how many voxels per fractal? That is, how fine a mathematical grid do we want to look at? Well, let’s have a nice big cubical display, ten meters on a side, with a resolution down to the smallest visible level, say to a tenth of a millimeter. And let’s also require that I can zoom down into the fractal by a factor of a ten million (which is a series of seven ten-fold zoom steps). So that comes to a resolution of a trillion voxels per edge, and I cube that for 10-to-the-36th-power voxels in all.
And I’ll iterate my fractal formulae a thousand times per voxel, so that makes 10-to-the-39th-power steps.
Suppose I’m looking at all the possible fractals specified by let us say, a degree five polynomial that uses complex-number parameters. So, if we don’t to the trouble of eliminating terms from the polynomial and we don’t take into account the constant term, that makes a total of ten real-number parameters, and evaluating the polynomial might take on the order of ten-squared steps. So now we’re looking at 10-to-the-41st-power steps to generate one of our degree-six fractals.

And, as I said, we’ll look at a wide range of the possible fractals of this kind—again assuming that we have some background algorithm to select the most aesthetically pleasing one.
For our search through the range of all the possible fractals of this kind, suppose that we let each of our ten real-number parameters vary between -5.0 and +5.0, stepping them along rather coarsely by increments of a thousandth. So each parameter is stepped through 10,000 values. And there are ten parameters, so I get 10,000 to the 10th-power combinations of values, that is, a number of combinations that’s 10-to-the-40th-power.
Multiplying this number of fractals times the number computational steps per fractal, we get 10-to-the-79th-power computational steps in the case where we use a degree five equation. So it takes ten seconds for a cubic meter of space computing flat out to show the “best” of the degree five fractals.
And now, as I mentioned, we’ll require that the display be updated in real time while some additional parameter is being smoothly varied. I want, as I said, a hundred updates per second. But each update takes ten seconds. Fine, I’ll throw a thousand cubic meters of space at my problem. That’s just a cube that’s ten meters on a side, so my display field is just large enough to compute my image in real time.

But now Hinton wants to crank up the degree! He’s not happy with degree five.
Suppose we specify some arbitrary degree that I’ll write in the form (N/2). This is an order N/2 polynomial with complex numbers as parameters and, therefore N real-number parameters to worry about. Evaluating the polynomial takes on the order of N-squared steps, and doing this a thousand times for our preferred voxel sizes makes for (10-to-the-36th times N-squared) steps.
And we step our parameters along at that same small increment we talked about above, the number of possible fractals of this kind are (10-to-the-4N-power).
So, all in all, if we go to a degree of the form (N/2), it takes (10-to-the-36th times N-squared times 10-to-the-4N-power) steps to generate all variations of the 3D fractals of this degree.
So if Hinton wants to look at fractals of degree 35, that means an N value of 70 parameters. So then our number of computations needed to show the best of these fractals is 10-to-the-36th-power times 70-squared times 10-to-the-280th-power. That means our product is going to be a number between 10-to-the-319th-power and 10-to-the-320th-power. Well over a googol-cubed.

ZZZT! System overload.
For, remember, Earth can only compute about a googol-squared operations per second, and the whole visible universe can only handle 10-to-the-229th-power!
Time to have a talk with those Solsols and Bulbers about borrowing googol-squared computations per second…