I recently acquired a copy of my old friend Clifford Pickover’s new tome, The Math Book , a really attractive and reasonably priced volume with 250 full page color illustrations, each illustration accompanied by a single-page description.
In Pickover’s words, “My goal in writing The Math Book is to provide a wide audience with a brief guide to important mathematical ideas and thinkers, with entries short enough to digest in a few minutes.”

[Breather Pseudosphere, Copyright (C) 2006 by Paul Nylander. See a larger image on Paul’s site.]
One of my favorite images in The Math Book is Paul Nylander’s rendition of the so-called Breather Pseudosphere. The idea behind this surface is that it has a constant curvature of -1, as opposed to a sphere, which might have a constant curvature of +1, and also as opposed to a plane, which has a constant curvature of 0. You’re supposed to ignore the ribs, and you need to accept that the surface intersects itself along a circle, which is clearer in the image below, by Xah Lee. You can rotate this image on Xah’s site.

[Segment of a Breather Pseudosphere, Copyright 2006 by Xah Lee.]
From the arcane math references that I’ve consulted—see for instance the Wikipedia “breather” page—I gather that the breather pseudosphere can in fact “breathe” in the sense that, by diddling a certain parameter, someone (not me anymore) could create a sequence of images of it and then assemble these into a video in which this negatively curved object will pulsate like some omnivorous space squid from Dimension Z. If any of you ultra-math-and-CS maniacs out there has access to such a video—or feels the urge to create one—share the link with us via a comment on this post!
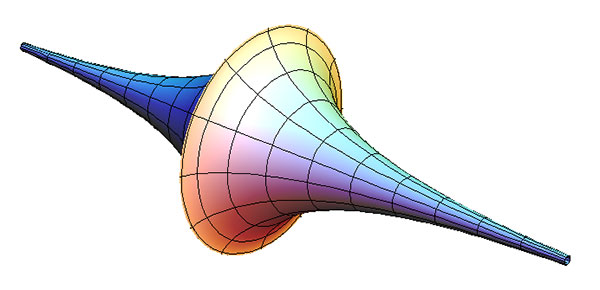
[A traditional Beltrami pseudosphere, Copyright (C) 2006 by Richard Palais and the the 3DXM consortium.]
As Pickover’s book explains, the notion of pseudospheres was invented in 1868 by the mathematician Eugenio Beltrami, who formulated the more familiar “double trumpet” model, as shown above, created by the 3DXM Consortium . (3DXM is a graphics program, now called 3D-XplorMath.)
You can find further images of various kinds of pseudospheres (these images by Xah Lee, Luc Bernard and other members of the 3DXM consortium) on the Gallery of Pseudospherical surfaces at the Virtual Math Museum. This page includes an essay “About Pseudospherical Surfaces,” which explains (amid much gnarly math) that, at least when depicted in our normal 3D space, any surface of constant curvature -1 will include “singularities” in the forms of self-intersections or cuspy lines where the surface has a crease in it—like those ribs in the breather pseudosphere or like the edge where Beltrami’s two trumpets meet. But you can smoothly embed pseudospheres into 4D space, I believe.

As I was discussing in an earlier post, another way to create a negatively curved space is to start with a disk of some ductile material, and the keep stretching the disk all over, but without overly stretching the outer edge. The inside of the disk acquires more area than one would find in a regular flat disk. The extra room is there because the interior is now a negatively curved surface. And I think this surface is something like a pseudosphere. (A different approach is to stretch the outer edge of the disk to infinite length, and this is a different model of negatively curved space called the Poincaré plane.)

[Copyright (C) 2009 by Vonda N. McIntyre . White hyperbolic anemone with red veins.]
Some knitters and beaders have crafted physical objects like the edge-stretched pseudosphere, some of which appear among a wild Crochet Reef show in 2009. Among the goodies on display was a bead construction of a pseudospherical sea anenome by no less a personage than the fantasy and SF writer Vonda N. McIntyre —see the MathCrafts section of her home page.

When I was snorkeling near Palau a few years ago, I noticed that many naturally occurring soft corals are indeed negatively curved surfaces.
It’s worth remembering, by the way, that if you’re living in a very small house, it might be nice to have negatively curved space inside…









August 29th, 2009 at 4:42 pm
Surely you mean, your small house should have a _positively_ curved space inside. Think of a bubble budding off of Flatland; big area, small Flatland circumference.
I particularly like the dodecahedral tessellation of hyperbolic 3-space. And of course the Poincare disk rules.
August 29th, 2009 at 5:19 pm
Paradoctor, geoemeters agree that it’s the negative curvature that gives you more area FOR A GIVEN RADIUS.
Think of it this way. I draw a circle with a fixed radius r. If the circle is in a flat space, it has area pi times r-squared and the circumference is two pi r.
But if the circle is on a sphere, the area of the cap inside it is LESS than pi times r-squared. And the circumference is LESS than 2 pi r. For if you were to stretch the cap out flat, it would get bigger.
If you draw the circle on a saddle then its area is bigger than pr r-squared as the circle is bent two different ways. And its circumference is bigger than two pi r.
So if I have a given fixed radius to work with for my house, it seems I want the innards to be negatively curved.
This said, let’s consider your point about the Flatland igloo. You’ve left the circumference fixed, but you’ve stretched both the area AND the radius. So, I guess one could argue that ANY kind of curved space inside a house of a fixed outer size will add more room. After all, it’s the flat space that’s a “minimal surface.”
So let me reiterate that it’s NOT the case that positive curvature is the ONLY ONE that gives “more area” for a fixed circumference. Negative curvature will also give “more area” within a given fixed circumference.
August 30th, 2009 at 6:02 am
Point taken about the radius. So for 2D surfaces, measured from inside, by radius, negative curvature gives more area, but measured from outside, by circumference, positive curvature gives more area. Interesting divergence. For 3D it is, respectively, radius, volume, and area.
September 1st, 2009 at 12:00 am
I checked out these comments on the web.
On the curvature of surfaces, Wikipedia has a great practical application example for Pizza
http://en.wikipedia.org/wiki/Theorema_egregium
I also looked on
http://demonstrations.wolfram.com
But didn’t see anything that was exactly as you describe above.
Do you have a link to an example on that site?
I’ve got Mathematica Player, so I can run the examples, …even if I
don’t fully understand them all.
September 15th, 2009 at 4:37 pm
I was wondering about the number of “ribs” in the breather pseudospheres, and what the lowest allowable number of ribs might be.
===========
Richard Palais responded with this image of breather pseudosphere with so few ribs as to be a Kuen surface and the text quoted below.
” Great Question ! !
” The breather surface has a parameter (called bb in the 3D-XplorMath version) that controls the “number” of ribs. Actually, for any choice of bb (in the allowed range 0 < bb < 1) there is really only a single rib that winds around the axis infinitely often while simultaneously winding around a circle in the plane perpendicular to the axis and centered on the axis; bb controls the relative rapidity with which the two windings occur. For certain values of bb, like 0.2, 0.4, 0.6, 0.8, the resulting "rib" is periodic, i.e., when it rotates once around the axis it returns to where it was, and in this case you get a nice clean surface. (Otherwise you get a mess unless you choose a relatively small parameter domain.) The version we use for the 3D-XplorMath icon (which you say has 22 ribs) corresponds to bb = 0.4. " For some reason I had never looked at what happens when bb is close to 1, although it is natural to wonder about that. So when you asked your question, I put bb = 0.995, and almost jumped out of my seat---for what 3D-XplorMath put on my screen was clearly a piece of the Kuen Surface, and after I adjusted the size of the parameter rectangle appropriately it became the standard version of Kuen. I have named it "BreatherAsKuen". I have never seen it mentioned anywhere that Kuen is a "special case" of Breather, and a quick Google search didn't turn anything up, so perhaps this is a new observation. Anyway, thanks for asking thw question." ===== Neil Bickford sent me a link to various versions of the pseudosphere as a short animation.
A video of the pseudosphere being wrapped with varying numbers of ribs arrived from Paul Nylander as well.