There’s a cute one-panel comic review of my novel Mathematicians in Love online today.

A programmer named Wiliam Rood has been emailing me about three- and four-dimensional Mandelbrot-set-like fractals. He has a mind-blowing, interactive demo on his page—the controls do work, but it takes a while to figure them out. Like using an alien iPhone that dropped out of a flying saucer.

I’ve been bugging Rood that he should be working with the Cubic Connectedness Map as described by Douady, Hubbard, Milnor, which is a different take on higher-dimensional fractals than one usually sees. If the images look like taffy, they’re using the Peitgen quaternion approach, which is, I think misguided. What I want to see is spherical warts on warts, as if the regular 2D Mandelbrot set were only a cross-sectional slice.

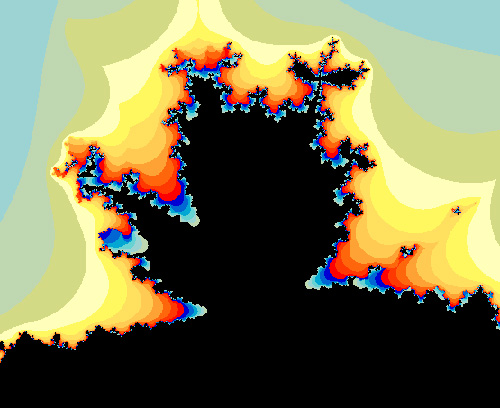
The cubic connectedness map lets you compute a 2D family of 2D cubic Mandelbrot sets Mk, where k ranges over the complext numbers. If you combined all of the Mk you’d have a 4D object, but first the thing ot look at is a 3D stack of them, like just vary one of the parameters inside k. You can stack to get a 3D object or animate to see a movie. I’d like to see the guy above opening his “mouth” and roaring.

You can also run a diagonalization of the Mk to get a single 2D set I modestly call the Rudy set. I put all of these cubic connectedness map fractals into the old Autodesk Chaos program, still available for free download (runs in a DOS window). And I explain the algorithms and the theory on my own alien-scribed tablet, which also has a link to Chaos program download.

I’ve also been looking at some great demos by Daniel Piker, click on the image agove to se a 4D rotation of a horse. He’s using some software packages called Processing and Rhino, and getting some nice four-dimensional rotation videos, quite unlike any I’ve seen before.

[I might mention that if you embed a vimeo clip on your web page, the page goes into a continous-download mode with the vimeo site, thereby slaving your page to the corporate masters—which is why I’m not embedding the video.]

That’s all for today. Qeep on Quackin.

This entry was posted on Monday, December 8th, 2008 at 10:39 am and is filed under Rudy's Blog. You can follow any responses to this entry through the RSS 2.0 feed. Both comments and pings are currently closed.