I’ve been busy with various projects this month.
As I mentioned before, I put a version of the code for my continuous-valued cellular automata (CA) program Capow on the ultrageek GitHub site.

Here’s a really nice image I made with a CA based on a so-called “activator-inhibitor rule with saturation.” You can see the detailed code for this rule online. And then I made a painting of this image, with things changing, as they do, along the way.

“Soft Zhabo” acrylic on canvas, March, 2017, 40” x 30”. Click for a larger version of the painting.
That guy near the top…is that kangaroo, or maybe a turtle with a lumpy head?

And I reread William Gibson’s wonderful novel, The Peripheral. One aspect I particularly admire about the work is how Bill sidesteps the perennial problem of how to have time travel without getting into such nasty paradoxes as these two chestnuts:
Yes and No: You go back in time and kill your past self as a teen. If you die, you don’t, and if you don’t you do.
Closed Causal Loop. You go back in time and give the blueprints of your time machine to your past self, who then builds the time machine that you’re using. So the time machine “invents itself.”

[“Death of the Hippie”, anonymous poster from Haight-Ashbury, 1967, now in “Summer of Love” show at De Young.]
In The Peripheral, someone has a device that sends and receives information, to and from the past. The act of making a connection produces a fork in causality, and the new branch no longer leads to the future that you are living in. The people in that now-forked-off past branch can affect your present, by doing things via the info link that you’ve set up. But they can’t change your branch’s past.
What gives this a nice time-travel aspect is that some of the characters have access to remotely operated “peripherals,” that is, android-like stand-ins. They’re not just emailing or videophoning to the future, they’re operating a robot that they’re (virtually) in. The heroine, Flynn, is from a down-at-the-heels country town in our time—it’s a Hillbilly Elegy type hamlet—and she gets a future peripheral which is very high-tech and well-equipped.

[Crab-like graffito on Ocean Beach.]
Conversely, the reluctant hero, an alkie named Netherton, and from a future version of London, gets a past peripheral which is a low-tech toy called a “Wheelie Boy.” The Wheelie Boy is like the push-toy a toddler might have, remotely operated, with a crude gyro to keep the handle erect, and a camera and a display screen atop the handle. Netherton can roll the Wheelie Boy around and look through the camera. And Flynne and her friends can see Netherton’s expressions on the Wheelie Boy’s display screen. Just one step up from a Face Time iPhone. But Gibson wonderfully conjures up what it would be like to be telepresent in the past.

Here’s a wonderfully touching scene of Netherton in Flynne’s room via Wheelie Boy.
Gloriously pre-posthuman. In a state of nature. … Her room, [with Netherton] rotating the cam as far as he could, was like the interior of some nomadic yurt. Nondescript furniture, tumuli of clothing, printed matter. This actual moment in the past, decades before his birth. A world he’d imagined, but now, somehow, in its reality, unimaginable. … He turned the camera, studying the shabby, shadowy tableau of lost domestic calm.

By the way, speaking of Bill’s “Wheelie Boy,” in the 70s, I drew cartoons about a character called “Wheelie Willie.” Sometimes when I read Gibson, I find odd little synchronicities. Chaotic eddies on the strange attractor that is cyberpunk. I have a old page of my Willie Willie cartoons on my blog.
One more touching line from The Peripheral, Flynne, wearing a high-tech peripheral in the future, sees some images in an antiques store.
“It was like the pictures in a box at a yard sale, nobody remembering who those people were, or even whose family, let alone how they came to be there. It gave her a sense of things falling, down some hole that had no bottom. Whole worlds falling, and maybe hers too.”

How deep a chord that strikes. If you’re of a certain age, you may have had this experience in sorting through a dead parent’s old photos and papers. Their past like decaying leaves on a forest floor.
Anyway, as I think I’ve mentioned, I’ve been working on a novella called “In the Lost City of Leng,” writing it with my old comrade Paul Di Filippo, who is in fact Rhodinsular (that is, from Rhode Island), as was our man H. P. L. We finished writing what is (one hopes) the final version of the story this week and sent it off to an SF magazine. Oh, and did I mention that I turned 71 this month?

Back to Lovecraft. I’ve been going through some of the stories in his collected works. “The Whisperer in Darkness” is a good one. Dig this condensed quote:
Tales of buzzing voices in imitation of human speech which made surprising offers to lone travelers on roads and cart-paths in the deep woods. They whispered at night in the forest with voices like a bee’s that tried to be like the voices of men—a morbid echo winging its way across unimaginable abysses from unimaginable outer hells. I can still hear that feeble, fiendish buzzing as it reached me for the first time. It was like the drone of some loathsome, gigantic insect ponderously shaped into the articulate speech of an alien species, and I am perfectly certain that the organs producing it can have no resemblance to the vocal organs of man, or indeed to those of any of the mammalia.

Back in the computer-hacking mode, riding the momentum of having restored CAPOW, I went ahead an posted a new free GitHub release of the source, manual, and executables of a 1991 Autodesk DOS program that was called “James Gleick’s CHAOS: The Software,” inspired by James Gleick and his brilliant book, Chaos: Making a New Science . The software was written by Josh Gordon, John Walker, and me. I wrote most of the algorithms, Walker did some fractal landscapes algorithms, and Josh Gordon did the interface, and much of the implementation of the algorithm code. The CHAOS program had six modules.
One of my favorites was a Mandelbrot Set program, incorporating: quadratic and cubic Julia sets, quadratic and cubic Mandelbrot sets, and a gnarly cubic connectedness map that I went ahead and named the Rudy set.
My other favorite CHAOS module was a Strange Attractors program showing the Lorenz Attractor, the Logistic Map, the Yorke Attractors, and the Henon Attractors.

The notion of strange attractors lies at the heart of chaos theory. Even now, nearly forty years later, the public at large still doesn’t get what chaos is about. You might try and summarize the main ideas like this:
* Although many natural and mathematical systems evolve according to clear mathematical equations, these systems tend not to be predictable.
* One reason for unpredictability is that any slight perturbation of the system is amplified into big changes later on. This is called sensitive dependence on initial conditions or the butterfly effect—stemming from the folkloric notion that our global weather is so sensitive that, say, the flap of a butterfly’s wing in the Amazon might be linked to a thunderstorm in Detroit a week later.
* A less obvious—and more fundamental—point is that many natural systems are inherently chaotic. The system never settles down. It dances among a wide gamut of values. When a natural system seems to wobble about, there often is not any “explanation.” It’s just being chaotic. That’s how the math happens to work.
* Another non-obvious but even more important point is that, even when a system is behaving chaotically, it’s values aren’t fully random. The unpredictable gamut of values tend to cluster into certain patterns. And these patterns are called strange attractors.The Mandelbrot set itself is a strange attractor for a certain simple process, and the images above are strange attractors as well.
The most famous strange attractor is the Lorenz attractor, as shown above.

[Frederic Church, “Rainstorm in the Tropics,” 1866, at DeYoung Museum]
Over time, I’ve learned to see strange attractors everywhere. The possible behaviors of the waves at the beach lie upon a large, multidimensional strange attractor that, over the years, I’ve become somewhat familiar with. The surf isn’t random. It’s not like you go out there and see a damp fog in the air instead of an ocean with waves. It’s not true that “anything’s possible.” It’s just that reality is very gnarly.

In his Chaos book, Gleick has a good line about strange attractors—he’s talking about a group of students/researchers who were at UC Santa Cruz in the late 70s and early 80s.
They had a game they would play, sitting at a coffeeshop. They would ask: How far away is the nearest strange attractor? Was it that rattling automobile fender? That flag snapping erratically in a steady breeze? A fluttering leaf? “You don’t see something until you have the right metaphor to let you perceive it.
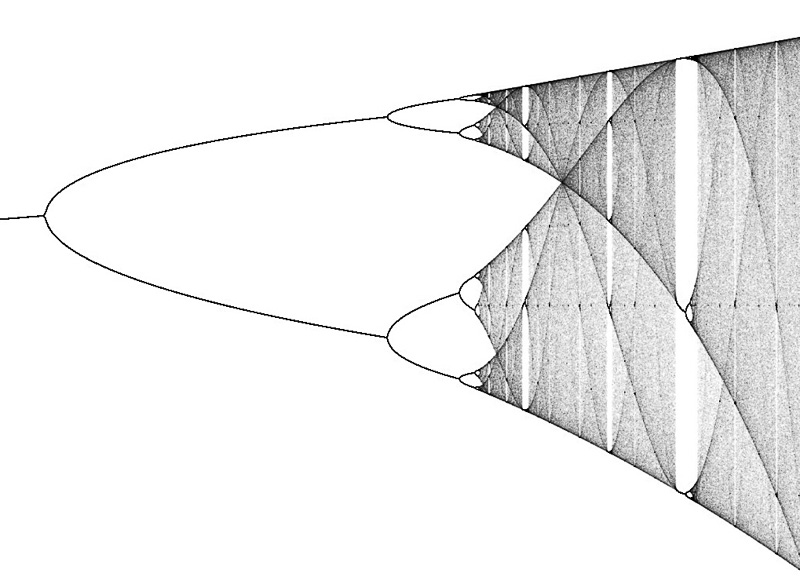
The above image of the “logistic map” illustrates a fifth fact about chaos. In this image, we imagine there being a parameter that is higher as you move from left to right. For each parameter value, the system’s values dances among the one or two or four or eight or zillion values directly above it. Each of those dances is a strange attractor. As the parameter’s value goes up, the strange attractor bifurcate into ever more complicated patterns. And then you hit full-on batshit pseudorandomicity. Mitchelll Feigenbaum discovered that each bifurcation comes about 4.67 times as fast. That’s “Feigenbaum’s contstant.”
* The transition from periodic to chaotic behavior has a universal quality, that is, we see the same kind of “period-doubling transition to chaos” for many types of systems, often with that same Feigenbaum constant involved.
Back to spotting strange attractors, the “Dynamical Systems Collective” at UC Santa Cruz included such now-legendary figures as Robert Shaw, Norman Packard, Jim Crutchfield, and Doyne Farmer. Gleick quotes a good line from Farmer:
“The same thing really drew all of us: the notion that you could have determinism but not really. The idea that all these classical deterministic systems we’d learned about could generate [seeming] randomness was intriguing. We were driven to understand what made that tick. … The idea that an equation could bounce around in an apparently random way—that was pretty exciting. … It seemed like something for nothing, or something out of nothing.”
Speaking of something for nothing, here’s a simulation of the ordinary water waves equation on a surface, which I ran on Capow and it made a really nice chaotic blob.

And here’s a painting inspired by that.

“Soft Zhabo” acrylic on canvas, March, 2017, 40” x 30”. Click for a larger version of the painting.
I call the painting “Alien Taxi,” because I’m imaging those two odd looking “people” being unsure about whether they should get into it. Winding back to an earlier memory, about fifteen years ago, Sylvia and I spent New Years’ Eve in San Francisco. We went out to the Beach Chalet for midnight, then got a late city bus back to our hotel near Union Square. At one point the bus stopped, and some very wasted guys were at the bus stop, and they got into an agitated discussion with each other as to whether the vehicle in front of them really was in fact a “bus,” or an alien vehicle. After a minute or two, our bus drove on without them. Going to Mars. Or to the year 2017.








