Today’s post is about the fourth dimension and about the nature of portals between parallel worlds.

As it happens, in Mach, 2013, there were not one but two classes being taught on the subject of the fourth dimension of space. And I was invited to give guest lectures at both these classes.

People sometimes dismiss the notion of the fourth dimension by saying, “Oh, that’s just time.” But mathematicians and SF writers are interested in a more bizarre kind of fourth dimension—an actual direction of space or, more properly speaking, a direction in hyperspace.

First, as I mentioned in my post of March 11, 2013, I gave a talk at Alan Weinstein’s mathematics of the fourth dimension class at Berkeley. They were using my very first book as a text, Geometry, Relativity, and the Fourth Dimension, by Rudolf v. B. Rucker. And then I gave a talk at Thomas Banchoff’s freshman level class on the fourth dimension at the University of San Francisco.

I recorded my talk at Banchoff’s class, talking about the fourth dimension of space, Edwin Abbott’s Flatland, and ideas about portals to parallel worlds. The podcast ends with a reading of the second half of my story, “Message Found In A Copy of Flatland,” which you can read online. You can find the recording of the talk at the link below, and I’ll say a bit more about the talk further down.

Banchoff has consulted with the artist Salvador Dali about his work. Dali famously included an unfolded hypercube in his painting Christus Hypercubicus, shown below. You can find a video of a full-length lecture by Banchoff on “The Four-Dimensional Geometry and Theology of Salvador Dali” online. Tom is giving a new version of this talk at University of San Francisco on April 18, 2013 at 11:45 am.

Banchoff invented that paper model of the hypercube shown in Dali’s painting. I was discussing this with him at lunch, and he said, “I have a paper model of a six-dimensional hyperhypercube folded up in my suitcase.” So we went to his office where he had the “suitcase” in which he keeps his lecture supplies.

Tom explained this model to me—bascially you use the three extra dimensions (4, 5, and 6) for bending the model around to glue together each of its opposite sides. If I didn’t grasp this as clearly as he did, that’s because he wrote his Ph.D. thesis on the model.

“I thought if it while I was folding shirts onto cardboards,” Tom told me. “I made the model and took it to my thesis advisor. He said, ‘You’ve found a gold mine.’”

Such a mathematician-style talk. Looking at that cardboard honeycomb and saying it’s a six-dimensional gold mine.

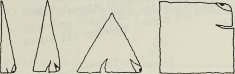
My talk depended on a timeworn analogy. 4:3 as 3:2. That is, in thinking about the mysterious fourth dimension, it helps to imagine a flat two-dimensional creature trying to imagine a third dimension. The flat creatures we usually talk about are Edwin Abbott’s Flatlanders.

The drawings I’m showing here were done by my artist friend David Povilaitis for my book, The Fourth Dimension, which is currently available in used editions only, but which is due to be reprinted in a new edition in 2014 or 2015. I’m sorry about the small size of the images I’m showing here today, but these are old scans, I didn’t want to rescan them.

One of the specific things I talked about was the nature of a portal to a parallel world. This is a commonplace in fantasy and SF movies—a magic door to another world. Dropping down to Flatland, we can think of the two worlds as being parallel “sheets” of space. The Flatlanders live on the lower world and some other flat creatures—let’s call them Globbers—live in the upper world.

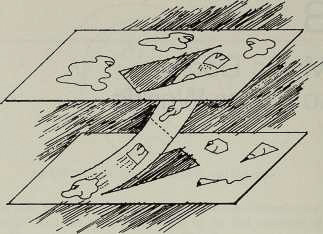
If we want to make the simplest kind of path between the worlds, we fold up a tab from the lower world and glue it to a tab from the upper world. This is what a door-like portal to another world is like. One problem here is that you need to be very careful not to slide off the edges of the path between the world. Or you might dissolve into Nothingness.

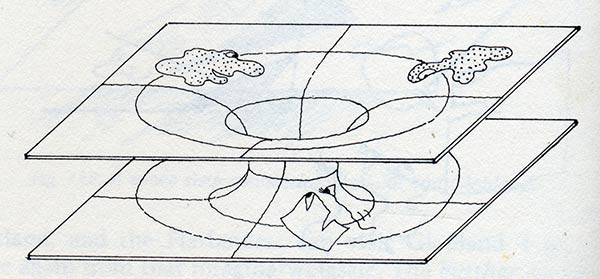
The right way to do it is to use what’s called an Einstein-Rosen bridge. You make a wormhole or throat that runs smoothly from one sheet of space to the other. In seeing this picture, people often worry that the Flatlanders who slide through the throat to the alternate world will end up on the “underside” of that space’s sheet. But you want to think of these sheets as having no thickness so that being on one side of the sheet is the same as being as the other. Or think of the sheets as soap-films with the Flatlanders and Globbers as being like colored patterns in the soap.

Moving up to an Einstein-Rosen bridge between two 3D universes, we can think of our 3D spaces as floating in a 4D hyperspace, and having a “bent” region that connects the spaces. And our 3D spaces have no essential 4D hyperthickness.

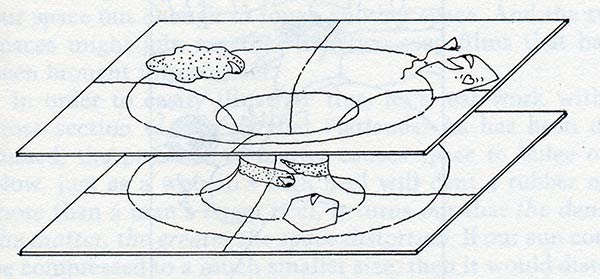
In The Fourth Dimension, my character A Square wants to go off to a private place with a Flatland woman called Una. She’s married a jealous Hexagon. In the two images above, we see Square and Una hesitating at the mouth of the ER Bridge. And in the second image, they’ve slid through the portal in the land of the Globbers, and a helpful Globber has wrapped himself around the throat of the ER bridge so that A Hexagon can’t see through.

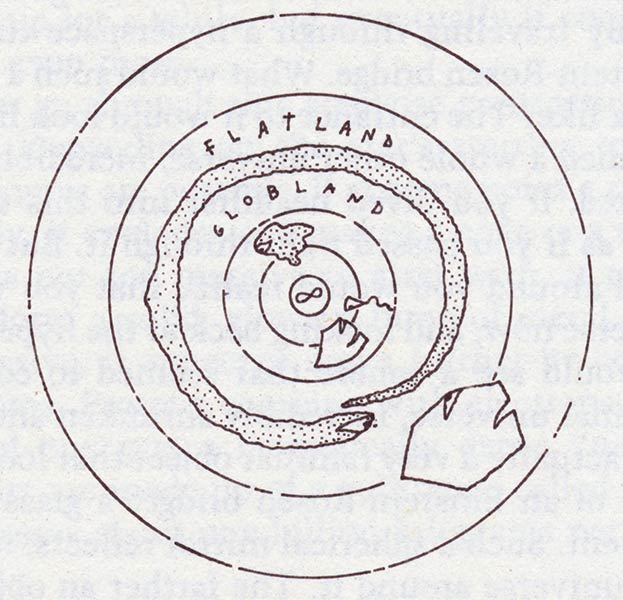
The image above shows how the situation looks to the 2D Hexagon. He views the mouth of the portal as a circle [in our version we’d see a sphere]. Globland lies within the circle, Flatland lies outside. And the point at infinity lies at the seeming center of the ball—that is, a whole endless world fits into the ball with everything getting smaller and smaller as it approaches the center.

In terms of our space, we can visualize an Einstein-Rosen bridge as resembling a shiny Christmas ornament ball, a sphere within which you seem to see whole world. There are two kickers if the “ball” is the mouth of an ER bridge to another world. (a) The world you see inside the ball isn’t the same as our world. (b) The ball doesn’t have a solid surface, it’s zone that you can walk or crawl through.

I describe an ER bridge in my story “The Last Einstein-Rosen Bridge,” which is also online as part of my Complete Stories. In the story, my character finds the portal lying in an asparagus field near Heidelberg, Germany.

I also describe an Einstein-Rosen bridge in my novel Realware, which is now in print as part of the four-volume The Ware Tetralogy, including Software, Wetware, Freeware, and Realware.

I’ll reprint a scene from Realware where my character Phil goes through an ER bridge, which he calls a “powerball.” In Phil’s case, what’s on the other side of the bridge is a small hyperspherical world, which is why he sees images of himself at the very end.

The powerball came in across the water, low down at Phil’s level, flying straight at him. Phil braced himself, wrapping his arms tight around his knees. The powerball looked like a big, glowing crystal ball, reflecting and refracting light, though not so smooth as a glass ball, perhaps a bit more like a drop of water.

As it drew closer there was an odd effect on the rest of the world: things seemed to melt and warp, distorting themselves away from the magic ball.

Closer and closer it came, yet taking an oddly long time to actually arrive. It was as if the space between Phil and the ball were stretching nearly as fast as the ball could approach. The ball was like a hole opening up in the world. Everything was being pushed aside by it; the sky and waves were being squeezed out along its edges.

Phil looked back over his shoulder; there was still a little zone of normality behind him—the nearest section of the rocky cliff s looked much the same. But so strong was the space warping of the powerball that the beach to the left and right seemed to bend away from him and, as Phil watched, this effect grew more pronounced. In a few moments it was as if Phil stood out on the tip of a little finger of reality, with the glowing powerball’s hyperspace squeezing in on every side. Back there at the other end of the finger, back in the world, Wubwub and Shimmer were peeking out of their cave entrance watching him, the cowards. He fought down an urge to run at them, and forced himself to turn back to face the engulfing ball. What could he see within the ball? Nothing but funhouse mirror reflections of himself: jiggling pink patches of his skin against a blue background filled with moons and stars—his shirt.

And then, like a mighty wave breaking, the warped zone moved over Phil. He felt a deep shock of pain throughout his body, as if something were pulling and stretching at his insides. His lungs, his stomach, his muscles, his brain—every tissue burned with agony.

“Phil! Phil!”

Phil didn’t dare turn; he felt as if the slightest motion might tear his innards in two. But, peering from his pain-wracked eyes, he realized there was no need to turn, for with the powerball centered on him, his view of the world had changed. The entire world was squeezed into a tiny ball that seemed to float a few feet away from him like a spherical mirror the size of a dinner plate. And there in the little toy world, like animated figurines, were Cobb and Yoke. Running toward him. Phil instinctively reached out towards them but—swish—something flashed past his fingers like an invisible scythe. And then—pop—the little bubble that had been the normal world winked out of view, and Phil was alone in the hypersphere of the powerball.

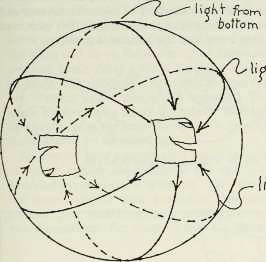
Phil’s guts snapped back to normal; the pain and its afterimage faded. He found himself comfortably floating within an empty, well-lit space that contained glowing air, his body and seemingly nothing else.

See you on the other side!

Added November 2, 2016:

I used an Einstein Rosen bridge again in my novel Million Mile Road Trip. I write about it in a June, 2016 post.

This entry was posted on Saturday, March 30th, 2013 at 9:25 am and is filed under Rudy's Blog. You can follow any responses to this entry through the RSS 2.0 feed. Both comments and pings are currently closed.