

Next: Continuous Valued Cellular
Up: Continuous Valued Cellular
Previous: FermiPasta, Ulam
Because of the discrete nature of computers, we can only approximate the
solution to a PDE at certain grid points on the 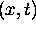 plane. We label these
points of approximation
plane. We label these
points of approximation 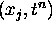 where
where 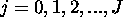 and
and 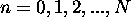 and employ the abbreviations
and employ the abbreviations 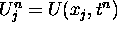 and
and 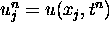 , where
, where
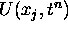 is the numerical approximation at the grid points of interest for
is the numerical approximation at the grid points of interest for
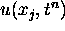 , the actual PDE solution. We are interested, of course, in making
, the actual PDE solution. We are interested, of course, in making
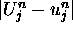 as small as possible. To accomplish this we must consider the
accuracy and the stability of our approximation scheme.
as small as possible. To accomplish this we must consider the
accuracy and the stability of our approximation scheme.
The accuracy of a scheme is really just a matter of minimizing the error term
in the Taylor appoximation for the scheme. Because of its simplicity --- and
its applicablity to eqns (7)-(9) --- we will use as an example the first order
linear traveling wave equation

From Taylor's formula we have that
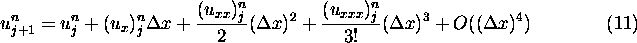
where 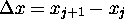 and also that
and also that
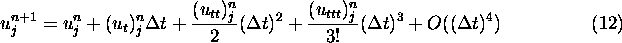
where 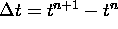 , so it follows that
, so it follows that
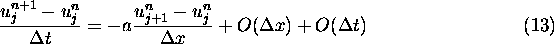
since the 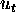 and the
and the 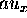 terms cancel by applying eq (10). This suggests
the following numerical algorithm to simulate eq (10):
terms cancel by applying eq (10). This suggests
the following numerical algorithm to simulate eq (10):
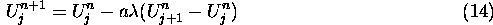
where 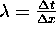 . This algorithm explicitly shows how to
compute values for a new time,
. This algorithm explicitly shows how to
compute values for a new time, 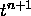 , given information at the current time,
, given information at the current time,
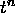 . To compute the value at a fixed time
. To compute the value at a fixed time 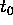 , the algorithm must be run
through
, the algorithm must be run
through
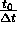 time steps. Since the error from each step is
time steps. Since the error from each step is 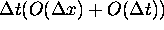 , the total error between the
computed solution and the actual solution at
, the total error between the
computed solution and the actual solution at 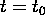 is
is 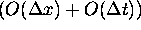 --- assuming that the errors from each time step can be added
together (which is not the case when the algorithm is unstable as we will soon
discuss). Due to the form of the total error (if the algorithm is stable), we
refer to the algorithm as being ``first order accurate in
x and first order accurate in t". If, instead of using the Taylor expansion in
eq (11), we use
--- assuming that the errors from each time step can be added
together (which is not the case when the algorithm is unstable as we will soon
discuss). Due to the form of the total error (if the algorithm is stable), we
refer to the algorithm as being ``first order accurate in
x and first order accurate in t". If, instead of using the Taylor expansion in
eq (11), we use
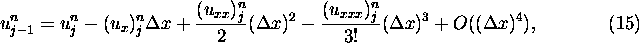
we end up with a similar numerical scheme that also is first order accurate in
both x and t:
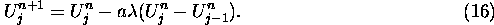
The scheme in eq (14) is called a downwind scheme; the scheme in eq
(15) is called an upwind scheme. We could also subtract eq (15) from eq
(11), which yields
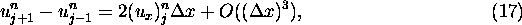
which implies that the numerical scheme
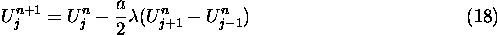
is first order accurate in time and second order accurate in space since the
error at a fixed time value is 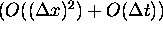 . Obviously,
one wishes to employ schemes with higher order errors since these schemes require
less grid points (and therefore less computational time) to obtain a computed
solution that is within a given error of the actual solution.
. Obviously,
one wishes to employ schemes with higher order errors since these schemes require
less grid points (and therefore less computational time) to obtain a computed
solution that is within a given error of the actual solution.
There is, however, more to numerical simulation of PDEs than just Taylor
expansions and accuracy questions. Consider eq (10) where the domain of
x is infinite and the initial condition 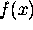 is specified:
is specified:
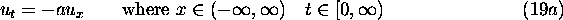

The unique solution to this equation is simply

In other words the value of the solution is constant along each line x=at +
C. These lines are called characteristic lines, and they occur when the
domain of x is finite as well as infinite. In other words the value of the
solution at a point depends only on which characteristic line crosses through
that point. If we consider x to be the abscissa and t the ordinate, then
each characteristic line has a positive slope of
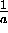 . The constant a is often referred to as the wave speed
since it specifies how fast a disturbance at a point x propagates down to
other values of x. Now consider what happens when we apply the downwind
scheme in eq (14) in an attempt to solve eq (10). The downwind scheme only uses
the points
. The constant a is often referred to as the wave speed
since it specifies how fast a disturbance at a point x propagates down to
other values of x. Now consider what happens when we apply the downwind
scheme in eq (14) in an attempt to solve eq (10). The downwind scheme only uses
the points
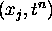 and
and
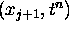 to estimate the value of the point
to estimate the value of the point
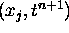 , but we know from the characteristic lines that the
value at this point only depends on the value of the solution at
, but we know from the characteristic lines that the
value at this point only depends on the value of the solution at 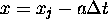 if
if 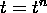 , which is outside the range of the two points being used. This
causes the computer generated solution using the downwind scheme to go haywire
and yield gibberish. One may wonder how can this happen since we know the
scheme is accurate. The answer is that accuracy only considers local
error, whereas the stability problem that is occuring in this case is a global
issue.
, which is outside the range of the two points being used. This
causes the computer generated solution using the downwind scheme to go haywire
and yield gibberish. One may wonder how can this happen since we know the
scheme is accurate. The answer is that accuracy only considers local
error, whereas the stability problem that is occuring in this case is a global
issue.
The Taylor series analysis of error in determining accuracy assumes that
the solution is correct at 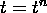 , and then finds the error that is created when
the solution at
, and then finds the error that is created when
the solution at 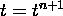 is approximated. However, if the error accrued in a
step is magnified by each subsequent step, we can no longer just add the
individual errors produced at each step; in fact, when the errors are magnified by
subsequent steps, we observe that the solution is unstable, that is, the global error
quickly blows up. When a scheme attempts to approximate the solution at a point\
is approximated. However, if the error accrued in a
step is magnified by each subsequent step, we can no longer just add the
individual errors produced at each step; in fact, when the errors are magnified by
subsequent steps, we observe that the solution is unstable, that is, the global error
quickly blows up. When a scheme attempts to approximate the solution at a point\
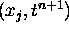 whose characteristic line crosses the
whose characteristic line crosses the
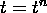 line outside the range of points used by the scheme, then the scheme, no
matter how accurate, will always magnify errors in each step and therefore be
unstable. In other words the numerical range of dependence must always contain
the theoretical range of dependence of the solution or instablity will occur.
This principle is called the CFL (Courant-Friedrichs-Lewy) condition (sometimes
referred to simply as the Courant condition) [7]. This guarantees that
the downwind scheme will always be unstable and that the upwind scheme can only
be stable if
line outside the range of points used by the scheme, then the scheme, no
matter how accurate, will always magnify errors in each step and therefore be
unstable. In other words the numerical range of dependence must always contain
the theoretical range of dependence of the solution or instablity will occur.
This principle is called the CFL (Courant-Friedrichs-Lewy) condition (sometimes
referred to simply as the Courant condition) [7]. This guarantees that
the downwind scheme will always be unstable and that the upwind scheme can only
be stable if 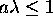 . Even if a scheme satisfies the CFL condition, it may
still be unstable, but we will not be analyzing any schemes that possess this
flaw in this paper.
. Even if a scheme satisfies the CFL condition, it may
still be unstable, but we will not be analyzing any schemes that possess this
flaw in this paper.
Before analyzing the FPU nonlinear wave equations, we wish to apply the above
analysis to the linear wave equation, 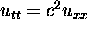 , where we use
, where we use
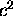 to denote the constant
to denote the constant 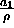 for reasons that will soon be
apparent. If we define
for reasons that will soon be
apparent. If we define 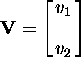 where
where 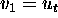 and
and 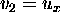 then we have that the wave equation is
satisfied,
then we have that the wave equation is
satisfied, 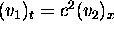 , and also that the mixed partials are equal,
, and also that the mixed partials are equal,
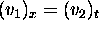 . This allows us to write the wave equation as the following
first order partial differential system:
. This allows us to write the wave equation as the following
first order partial differential system:
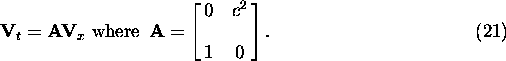
Eq (21), of course, is just the matrix form of the travelling wave equation from
eq (10), and its solution contains many of the same properties as eq (10). As
opposed to the solution depending upon one characteristic line, the solution,
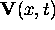 , now depends on two characteristic lines whose wave speeds
are c and -c, the eigenvalues of
, now depends on two characteristic lines whose wave speeds
are c and -c, the eigenvalues of 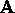 . Therefore the slopes of the
two characteristic lines are the reciprocals of the wave speeds,
. Therefore the slopes of the
two characteristic lines are the reciprocals of the wave speeds,  and
and 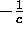 . As before, we must satisfy the CFL stability condition, so we
now require that
. As before, we must satisfy the CFL stability condition, so we
now require that
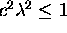 .
.
All that remains is to find a sufficiently accurate scheme. To obtain an
approximation for 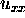 we add eq (11) to eq (15), yielding
we add eq (11) to eq (15), yielding
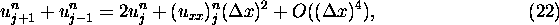
which we can combine with the analogous expression from the Taylor
expansions with respect to time to yield the numerical scheme
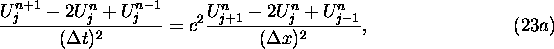
which we can reexpress as
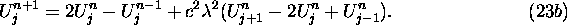
We note that this scheme is 2nd order accurate with respect to both time and
space.
We are now ready to consider the nonlinear FPU equations. We begin with the
quadratic FPU equation

where 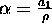 and
and 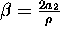 . (Note that
. (Note that 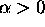 since
since 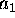 , like the spring constant k, is always positive in any realistic spring
model.) As with the linear wave equation we can rewrite eq (24) in vector form, but
now the matrix A will depend upon the value of
, like the spring constant k, is always positive in any realistic spring
model.) As with the linear wave equation we can rewrite eq (24) in vector form, but
now the matrix A will depend upon the value of
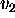 :
:
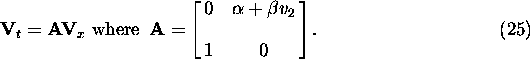
The wave speeds of the two characteristics are still the eigenvalues of
A, which are 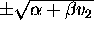 . (Note that we require
. (Note that we require 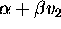 to be
positive since otherwise the wave speeds would be imaginery and the partial
differential equation would no longer be hyperbolic, which leads to equations beyond
our analysis here and causes the scheme to become unstable). Since the speeds are
functions of
to be
positive since otherwise the wave speeds would be imaginery and the partial
differential equation would no longer be hyperbolic, which leads to equations beyond
our analysis here and causes the scheme to become unstable). Since the speeds are
functions of
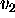 , that means the speeds vary, which implies that the characteristics are now
curves whose slopes vary as they progress in time as opposed to being straight lines
as was the case in the linear wave equation. This leads to a stability problem as
the CFL condition now requires that
, that means the speeds vary, which implies that the characteristics are now
curves whose slopes vary as they progress in time as opposed to being straight lines
as was the case in the linear wave equation. This leads to a stability problem as
the CFL condition now requires that
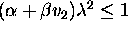 . If
. If 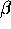 is small compared to
is small compared to
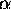 , then
, then 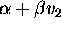 will be positive and the variations in
will be positive and the variations in 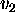 may not be
severe enough to violate the CFL condition, but if the nonlinearity becomes more
significant, which means the value of
may not be
severe enough to violate the CFL condition, but if the nonlinearity becomes more
significant, which means the value of 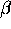 becomes larger, eventually the CFL
condition will be violated (or
becomes larger, eventually the CFL
condition will be violated (or 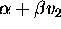 will become nonpositive) and
the scheme will become unstable. (Note: in the experiments in section 5, we will set
will become nonpositive) and
the scheme will become unstable. (Note: in the experiments in section 5, we will set
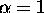 and use values of
and use values of 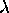 that are slightly smaller than 1 which will
cause the CFL condition to be violated before
that are slightly smaller than 1 which will
cause the CFL condition to be violated before 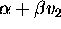 becomes nonpositive.)
Since by definition
becomes nonpositive.)
Since by definition
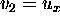 , we see that if
, we see that if
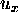 gets large not only does the numerical scheme become unstable, but also
the underlying differential equation becomes less valid since higher order terms
in the Taylor approximation given in eq (4) start to become significant.
gets large not only does the numerical scheme become unstable, but also
the underlying differential equation becomes less valid since higher order terms
in the Taylor approximation given in eq (4) start to become significant.
The analysis for the cubic FPU equations is similar. We now have that

where 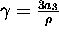 , which can be expressed in matrix form as
, which can be expressed in matrix form as
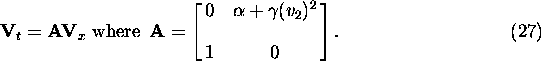
The corresponding CFL condition is 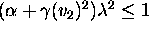 . Note
that if
. Note
that if 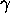 is positive, the wave speeds will be real and we will always have
a hyperbolic differential equation.
is positive, the wave speeds will be real and we will always have
a hyperbolic differential equation.
There are numerous accurate schemes that one can apply in the region where
the algorithm is stable. To simulate the quadratic FPU equation, eq (8), we can
combine eq (17) with eq (23) to form
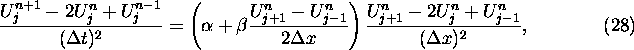
which can be rewritten as a scheme which is second order accurate in time and space:
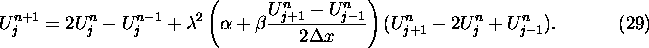
Eq (28) is a generalization of the FPU quadratic scheme (eq (ii)).
After setting 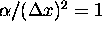 and
and 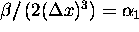 , one
can quickly establish that the right hand sides of eq (28) and eq (ii) are
identical.
, one
can quickly establish that the right hand sides of eq (28) and eq (ii) are
identical.
Similary, we can simulate the cubic FPU equation, eq (9), by again combining eq (17)
with eq (23) to obtain the following second order accurate scheme:
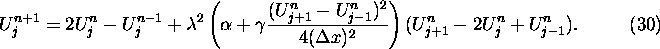
The fact that the scheme in eq (30) is not the same as FPU's cubic scheme (eq
(iii)) does not pose a problem. Either FPU's scheme or eq (30) can be used to
simulate the cubic FPU equation as both schemes are second order accurate and will
therefore produce essentially equally valid simulations. (The second order accuracy
of the FPU's cubic scheme is quickly established using Taylor series.)
There is another phenomenon that is important in nonlinear hyperbolic partial
differential equations. Because the characteristics are curves, characteristics
within a family can intersect each other. (In the linear case, each family of
characteristic lines has a constant slope:  for one family,
for one family,
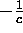 for the other family.) When the characteristics intersect, a
shock, i.e., a discontinuity in the solution, occurs. While multiple weak
solutions to the nonlinear equation are possible, one usually desires to simulate
the unique observed solution that the phenomena being modeled exhibits. For most
physical phenomena the solution of interest is the Lax entropy solution of the
equation, which can be simulated using monotone schemes [8]. A particularly nice
introduction to shock capturing monotone schemes is presented in [9].
for the other family.) When the characteristics intersect, a
shock, i.e., a discontinuity in the solution, occurs. While multiple weak
solutions to the nonlinear equation are possible, one usually desires to simulate
the unique observed solution that the phenomena being modeled exhibits. For most
physical phenomena the solution of interest is the Lax entropy solution of the
equation, which can be simulated using monotone schemes [8]. A particularly nice
introduction to shock capturing monotone schemes is presented in [9].
We do not pursue these schemes here, however, as we are interested in other
aspects of the transition to instability.


Next: Continuous Valued Cellular
Up: Continuous Valued Cellular
Previous: FermiPasta, Ulam
Rudy Rucker
Sat May 9 20:21:15 MET DST 1998
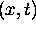 plane. We label these
points of approximation
plane. We label these
points of approximation 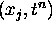 where
where 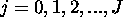 and
and 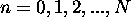 and employ the abbreviations
and employ the abbreviations 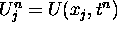 and
and 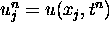 , where
, where
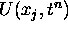 is the numerical approximation at the grid points of interest for
is the numerical approximation at the grid points of interest for
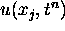 , the actual PDE solution. We are interested, of course, in making
, the actual PDE solution. We are interested, of course, in making
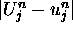 as small as possible. To accomplish this we must consider the
accuracy and the stability of our approximation scheme.
as small as possible. To accomplish this we must consider the
accuracy and the stability of our approximation scheme.

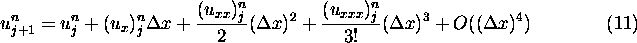
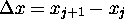 and also that
and also that
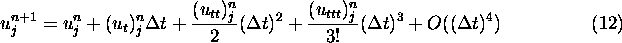
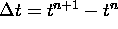 , so it follows that
, so it follows that
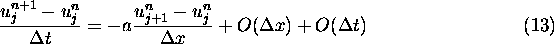
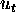 and the
and the 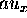 terms cancel by applying eq (10). This suggests
the following numerical algorithm to simulate eq (10):
terms cancel by applying eq (10). This suggests
the following numerical algorithm to simulate eq (10):
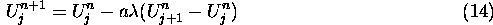
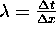 . This algorithm explicitly shows how to
compute values for a new time,
. This algorithm explicitly shows how to
compute values for a new time, 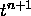 , given information at the current time,
, given information at the current time,
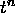 . To compute the value at a fixed time
. To compute the value at a fixed time 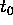 , the algorithm must be run
through
, the algorithm must be run
through
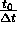 time steps. Since the error from each step is
time steps. Since the error from each step is 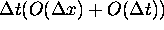 , the total error between the
computed solution and the actual solution at
, the total error between the
computed solution and the actual solution at 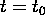 is
is 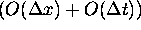 --- assuming that the errors from each time step can be added
together (which is not the case when the algorithm is unstable as we will soon
discuss). Due to the form of the total error (if the algorithm is stable), we
refer to the algorithm as being ``first order accurate in
x and first order accurate in t". If, instead of using the Taylor expansion in
eq (11), we use
--- assuming that the errors from each time step can be added
together (which is not the case when the algorithm is unstable as we will soon
discuss). Due to the form of the total error (if the algorithm is stable), we
refer to the algorithm as being ``first order accurate in
x and first order accurate in t". If, instead of using the Taylor expansion in
eq (11), we use
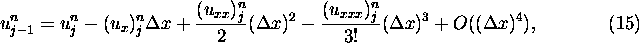
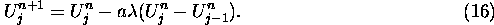
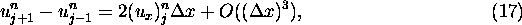
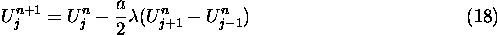
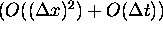 . Obviously,
one wishes to employ schemes with higher order errors since these schemes require
less grid points (and therefore less computational time) to obtain a computed
solution that is within a given error of the actual solution.
. Obviously,
one wishes to employ schemes with higher order errors since these schemes require
less grid points (and therefore less computational time) to obtain a computed
solution that is within a given error of the actual solution.
 is specified:
is specified:
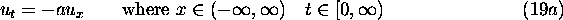


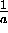 . The constant a is often referred to as the wave speed
since it specifies how fast a disturbance at a point x propagates down to
other values of x. Now consider what happens when we apply the downwind
scheme in eq (14) in an attempt to solve eq (10). The downwind scheme only uses
the points
. The constant a is often referred to as the wave speed
since it specifies how fast a disturbance at a point x propagates down to
other values of x. Now consider what happens when we apply the downwind
scheme in eq (14) in an attempt to solve eq (10). The downwind scheme only uses
the points
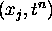 and
and
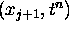 to estimate the value of the point
to estimate the value of the point
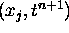 , but we know from the characteristic lines that the
value at this point only depends on the value of the solution at
, but we know from the characteristic lines that the
value at this point only depends on the value of the solution at 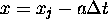 if
if 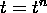 , which is outside the range of the two points being used. This
causes the computer generated solution using the downwind scheme to go haywire
and yield gibberish. One may wonder how can this happen since we know the
scheme is accurate. The answer is that accuracy only considers local
error, whereas the stability problem that is occuring in this case is a global
issue.
, which is outside the range of the two points being used. This
causes the computer generated solution using the downwind scheme to go haywire
and yield gibberish. One may wonder how can this happen since we know the
scheme is accurate. The answer is that accuracy only considers local
error, whereas the stability problem that is occuring in this case is a global
issue.
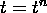 , and then finds the error that is created when
the solution at
, and then finds the error that is created when
the solution at 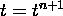 is approximated. However, if the error accrued in a
step is magnified by each subsequent step, we can no longer just add the
individual errors produced at each step; in fact, when the errors are magnified by
subsequent steps, we observe that the solution is unstable, that is, the global error
quickly blows up. When a scheme attempts to approximate the solution at a point\
is approximated. However, if the error accrued in a
step is magnified by each subsequent step, we can no longer just add the
individual errors produced at each step; in fact, when the errors are magnified by
subsequent steps, we observe that the solution is unstable, that is, the global error
quickly blows up. When a scheme attempts to approximate the solution at a point\
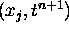 whose characteristic line crosses the
whose characteristic line crosses the
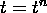 line outside the range of points used by the scheme, then the scheme, no
matter how accurate, will always magnify errors in each step and therefore be
unstable. In other words the numerical range of dependence must always contain
the theoretical range of dependence of the solution or instablity will occur.
This principle is called the CFL (Courant-Friedrichs-Lewy) condition (sometimes
referred to simply as the Courant condition) [7]. This guarantees that
the downwind scheme will always be unstable and that the upwind scheme can only
be stable if
line outside the range of points used by the scheme, then the scheme, no
matter how accurate, will always magnify errors in each step and therefore be
unstable. In other words the numerical range of dependence must always contain
the theoretical range of dependence of the solution or instablity will occur.
This principle is called the CFL (Courant-Friedrichs-Lewy) condition (sometimes
referred to simply as the Courant condition) [7]. This guarantees that
the downwind scheme will always be unstable and that the upwind scheme can only
be stable if 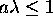 . Even if a scheme satisfies the CFL condition, it may
still be unstable, but we will not be analyzing any schemes that possess this
flaw in this paper.
. Even if a scheme satisfies the CFL condition, it may
still be unstable, but we will not be analyzing any schemes that possess this
flaw in this paper.
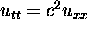 , where we use
, where we use
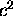 to denote the constant
to denote the constant 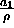 for reasons that will soon be
apparent. If we define
for reasons that will soon be
apparent. If we define 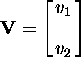 where
where 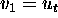 and
and 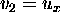 then we have that the wave equation is
satisfied,
then we have that the wave equation is
satisfied, 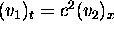 , and also that the mixed partials are equal,
, and also that the mixed partials are equal,
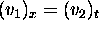 . This allows us to write the wave equation as the following
first order partial differential system:
. This allows us to write the wave equation as the following
first order partial differential system:
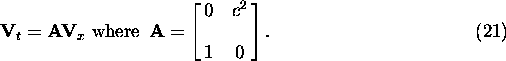
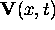 , now depends on two characteristic lines whose wave speeds
are c and -c, the eigenvalues of
, now depends on two characteristic lines whose wave speeds
are c and -c, the eigenvalues of 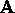 . Therefore the slopes of the
two characteristic lines are the reciprocals of the wave speeds,
. Therefore the slopes of the
two characteristic lines are the reciprocals of the wave speeds,  and
and 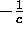 . As before, we must satisfy the CFL stability condition, so we
now require that
. As before, we must satisfy the CFL stability condition, so we
now require that
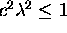 .
.
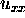 we add eq (11) to eq (15), yielding
we add eq (11) to eq (15), yielding
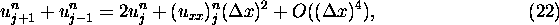
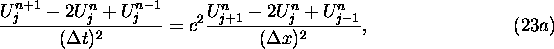
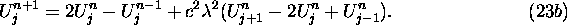

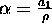 and
and 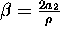 . (Note that
. (Note that 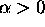 since
since 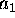 , like the spring constant k, is always positive in any realistic spring
model.) As with the linear wave equation we can rewrite eq (24) in vector form, but
now the matrix A will depend upon the value of
, like the spring constant k, is always positive in any realistic spring
model.) As with the linear wave equation we can rewrite eq (24) in vector form, but
now the matrix A will depend upon the value of
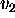 :
:
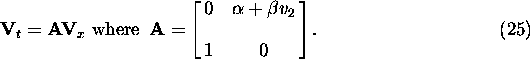
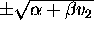 . (Note that we require
. (Note that we require 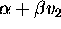 to be
positive since otherwise the wave speeds would be imaginery and the partial
differential equation would no longer be hyperbolic, which leads to equations beyond
our analysis here and causes the scheme to become unstable). Since the speeds are
functions of
to be
positive since otherwise the wave speeds would be imaginery and the partial
differential equation would no longer be hyperbolic, which leads to equations beyond
our analysis here and causes the scheme to become unstable). Since the speeds are
functions of
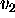 , that means the speeds vary, which implies that the characteristics are now
curves whose slopes vary as they progress in time as opposed to being straight lines
as was the case in the linear wave equation. This leads to a stability problem as
the CFL condition now requires that
, that means the speeds vary, which implies that the characteristics are now
curves whose slopes vary as they progress in time as opposed to being straight lines
as was the case in the linear wave equation. This leads to a stability problem as
the CFL condition now requires that
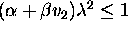 . If
. If 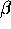 is small compared to
is small compared to
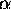 , then
, then 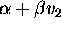 will be positive and the variations in
will be positive and the variations in 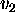 may not be
severe enough to violate the CFL condition, but if the nonlinearity becomes more
significant, which means the value of
may not be
severe enough to violate the CFL condition, but if the nonlinearity becomes more
significant, which means the value of 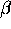 becomes larger, eventually the CFL
condition will be violated (or
becomes larger, eventually the CFL
condition will be violated (or 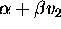 will become nonpositive) and
the scheme will become unstable. (Note: in the experiments in section 5, we will set
will become nonpositive) and
the scheme will become unstable. (Note: in the experiments in section 5, we will set
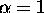 and use values of
and use values of 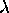 that are slightly smaller than 1 which will
cause the CFL condition to be violated before
that are slightly smaller than 1 which will
cause the CFL condition to be violated before 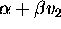 becomes nonpositive.)
Since by definition
becomes nonpositive.)
Since by definition
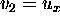 , we see that if
, we see that if
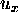 gets large not only does the numerical scheme become unstable, but also
the underlying differential equation becomes less valid since higher order terms
in the Taylor approximation given in eq (4) start to become significant.
gets large not only does the numerical scheme become unstable, but also
the underlying differential equation becomes less valid since higher order terms
in the Taylor approximation given in eq (4) start to become significant.

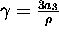 , which can be expressed in matrix form as
, which can be expressed in matrix form as
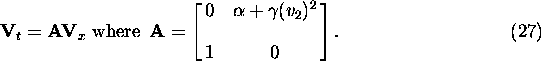
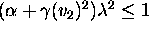 . Note
that if
. Note
that if 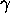 is positive, the wave speeds will be real and we will always have
a hyperbolic differential equation.
is positive, the wave speeds will be real and we will always have
a hyperbolic differential equation.
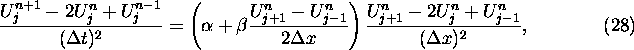
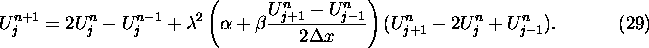
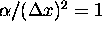 and
and 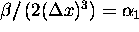 , one
can quickly establish that the right hand sides of eq (28) and eq (ii) are
identical.
, one
can quickly establish that the right hand sides of eq (28) and eq (ii) are
identical.
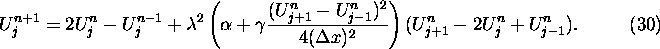
 for one family,
for one family,
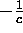 for the other family.) When the characteristics intersect, a
shock, i.e., a discontinuity in the solution, occurs. While multiple weak
solutions to the nonlinear equation are possible, one usually desires to simulate
the unique observed solution that the phenomena being modeled exhibits. For most
physical phenomena the solution of interest is the Lax entropy solution of the
equation, which can be simulated using monotone schemes [8]. A particularly nice
introduction to shock capturing monotone schemes is presented in [9].
for the other family.) When the characteristics intersect, a
shock, i.e., a discontinuity in the solution, occurs. While multiple weak
solutions to the nonlinear equation are possible, one usually desires to simulate
the unique observed solution that the phenomena being modeled exhibits. For most
physical phenomena the solution of interest is the Lax entropy solution of the
equation, which can be simulated using monotone schemes [8]. A particularly nice
introduction to shock capturing monotone schemes is presented in [9].