
by Rudy Rucker
April 2, 2010

RudyRockets (detail of the Rudy Set)
I gave an early version of this talk at the Computer Systems Laboratory Colloquium Stanford University twenty years ago, on March 7, 1990, as "Computing Sections of the Cubic Connectedness Map." Some of this information also appeared in the manual for the James Gleick's CHAOS program.
All the fractals discussed here can be viewed with CHAOS software. But CHAOS is unusable on the newer versions of Windows (starting with XP Service Pack 3 and including Windows 7). So this week, I've been porting my favorite algorithms to the Ultra Fractal platform, and this page describes the formulas and how to view them.
To run these fractals on Ultra Fractal, download a copy of Ultra Fractal 5 --- at the very least you can get a free, fully featured, evaluation copy that's good for a month.( The evaluation copy is fully functional except that if you export an image with it the image will be defaced with the words "Evaluation Copy.")
To see my Ultra Fractal implemenations, you can just download all of the Ultra Fractal public formulas by clicking Update Public Formulas on the Options menu of the Ultra Fractal program.
My two files are text files rvr.ufm and rvr.upr. "rvr" stands for me, Rudy von Bitter Rucker. The rvr.ufm file is a "formula" file that has the algorithms for the Cubic Julia, Cubic Mandelbrot, and Rudy sets written out in the pseudocode language used by Ultra Fractal, the "fm" stands for formula. The rvr.upr file holds several sets of parameters for various fractals using my formulas. the "pr" stands for parameter. Once you get the two files into the same directory, use Ultra Fractal to open the Parameter File rvr.upr, and then click on the thumbnails or names of the included fractals you want to see.
You can examine the formulas and parameters online at the Ultra Fractal "Browse Database" page. Scroll down to "Rudy Rucker." If you don't want the whole public formula database, you can save my files as text files with the ufm and upr extensions from there. Here is a direct links to the formula file rvr.ufm and the parameter file rvr.upr.

Detail of the MandelCubicWhoopDiDoo Cubic Mandelbrot Set
A map in the plane is some system for finding an image P' of each point P. One might, for instance, stretch the plane by moving each P twice as far from the origin O, or one might rotate the plane, moving each point P to a point P' some fixed number of degrees further clockwise.
If we think of each point in the plane as a complex number z = x + iy, one can get a very interesting map by taking z into z^2. In terms of points, the operation of letting P' be the square of P works by actually squaring the length from P to the origin and by then rotating P to P' in such a way that the angle between OP' and the x-axis is exactly twice the angle between OP and the x-axis.
If f is a map in the plane, and f maps z into z', I can express this either by writing z' = f(z) or by writing z --f--> z'. Given an f and a z, we can define a sequence zn by:
z0 = z
zn+1 = f(zn).
In terms of f,
z --f--> z1 --f--> z2 --f--> z3 --f--> z4 --f--> ...
The norm |z| of z = x + iy is gotten as sqrt(x^2 + y^2) and is equal to the distance of z from the origin. If |zn| becomes arbitrarily large as n increases, we say that z goes to infinity under the map f, which we can symbolize as z --f--> INFINITY. If z does not go to infinity under the map f, we write z --f--> FINITE and say that z is bounded under the map f. Note that z--f--> FINITE does not meant that the zn sequence approaches a specific limit; more characteristically, the zn will cycle among being close to some finite number of different limits. z--f--> FINITE simply means that there exists some real BOUND so that for all n |zn| < BOUND...typically BOUND is some small real number like 2 or 4.
You can skip past the next block if you already know about Quadratic Julia and Mandelbrot sets.
Review: Quadratic Julia and Mandelbrot Sets
Quadratic Julia Sets
The Julia set for a map f is defined as the set of all z in the plane which are bounded under f. Symbolically, the Julia set for f is { z : z --f--> FINITE )}.
The map fc given by fc(z) = z^2 + c has been widely studied. By changing one's coordinate system, any quadratic map A*w^2 + B*w + C can be put into the form z^2 + c, with z a linear function of w. We give the Julia set for fc the name Jc.
Jc = { z : z--fc--> FINITE }.
All the Jc are symmetric about the origin, meaning that if the complex number z = x + iy is in Jc, then the complex number -z = -x - iy is in Jc as well. Some of them are connected with non-empty interiors (disklike), some are connected with empty interiors (linelike),and the others are totally disconnected (dustlike) --- as shown from left to right below.
Jc being totally disconnected means that if A and B are in Jc, there is a disk around A which hits no member of Jc and which excludes B. No Julia set ever breaks into two or more disklike pieces to be partly disconnected without being totally disconnected and dustlike. Given this fact and the fact that the Jc have symmetry around the origin, it's not too surprising to learn that Jc is connected if and only if the origin (0,0) is a member of Jc.
The Quadratic Mandelbrot SetIf we think of varying c through all its complex values, we can think of a c-plane which has a Jc set defined at each of its points. Benoit Mandelbrot had the idea of looking at the locus of all the c's for which Jc is connected. This is the Mandelbrot set, M. Symbolically,
M = { c : Jc is connected}
M = { c : the origin is in Jc }, because Jc is connected iff (0,0) in Jc)
M = { c : c is in Jc }, because if z0 = (0,0) then z1 = f(z0) = c.
M = { c : c --fc--> FINITE }, by the definition of Jc.The last definition of the Mandelbrot set corresponds to the way we actually compute it. Each pixel position on the screen is identified with a distinct complex number c = u + iv. We set
z0 = c,
z1 = c^2 + c,
z2 = (z1)^2 + c, and so on...We repeat this process up to MAXITERATION times, where MAXITERATION is set as a program parameter to be maybe two thousand. After each step we check the value of |zn| against a value BOUND. The value of BOUND which we sometimes use for Mandelbrot sets is the square root of seven. One can prove that if |zn| passes BOUND, then |zn| will go on and get arbitrarily large as n increases.
If |zn| passes BOUND for some value of n less than MAXITERATION, then we give the pixel a color based on the value of n. And if |zn| stays less than BOUND for every value of n up through MAXITERATION, then we assume that the pixel represents a point inside the Mandelbrot set, and we typically color these points black.
Okay, now for the new stuff!!!
The maps which the Cubic Julias and Cubic Mandelbrots are based on have the form fkc, with
fkc(z) = z^3 - 3*k*z + c
As it happens, by moving the origin our coordinate system, any generalized cubic map can
be put into this form, that is, we don't need to have a z^2 term. The reason that I chose to write the the linear coefficient in the form -3*k has to do with making the computation run more smoothly.) For each fkc we
can define a cubic Julia set Jkc by:
Jkc = { z: z--fkc-->FINITE }.
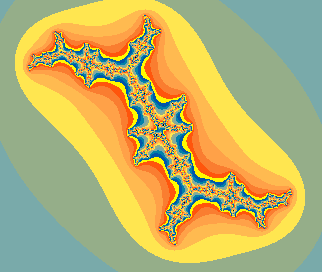
Unlike in the quadratic case, these Julia sets are generally not symmetric. Some of them are connected, like these two:

JuliaCubicAsteroids

JuliaCubicTwirly
some are connected but not totally disconnected (made of numerous separate connected patches) like this one:
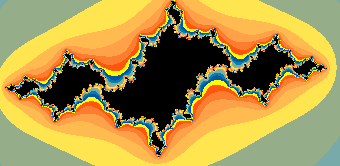
JuliaCubicChunks
and some are totally disconnected, like clouds of dust.
It has been proved that Jkc is in fact connected if and only if both the complex numbers k = a +ib and -k = -a -ib are in Jkc. As Jkc is not symmetric, it may happen that only one of k or -k is in Jkc. Jkc is connected only when both of these critical points are in Jkc.
The four-dimensional set of all complex pairs k and c such that Jkc is connected is known as the Cubic Connectedness map, or the CCM. This set has been studied by Adrian Douady, John Hubbard and John Milnor. See the technical papers by Adrian Douady and John Hubbard, “On the Dynamics of Polynomial-like Mappings, and by Bodil Branner and John Hubbard, The iteration of cubic polynomials Part I, and The iteration of cubic polynomials Part II: Patterns and parapatterns. I don't understand why this set isn't much better known!
CCM = { (k,c) : Jkc is connected}
or, putting it differently,
CCM = { (k,c) : ( k --fkc--> FINITE ) AND ( -k --fkc--> FINITE ) }
The way our program depicts the CCM is to show various two-dimensional cross-sections of it. These cross-sections are what we call Cubic Mandelbrot sets. If, for instance, k is fixed, then we can look at the Cubic Mandelbrot set Mk.
Mk = { c : Jkc is connected}
Mk
= { c : ( k--fkc-->FINITE ) AND ( -k--fkc-->FINITE ) }.
It turns out that that Mk is symmetric around the origin, that is, if c is in Mk, so is -c. And it also seems to be the case that whenever the origin is in Mk, then Mk is connected, and doesn't break into multiple pieces.
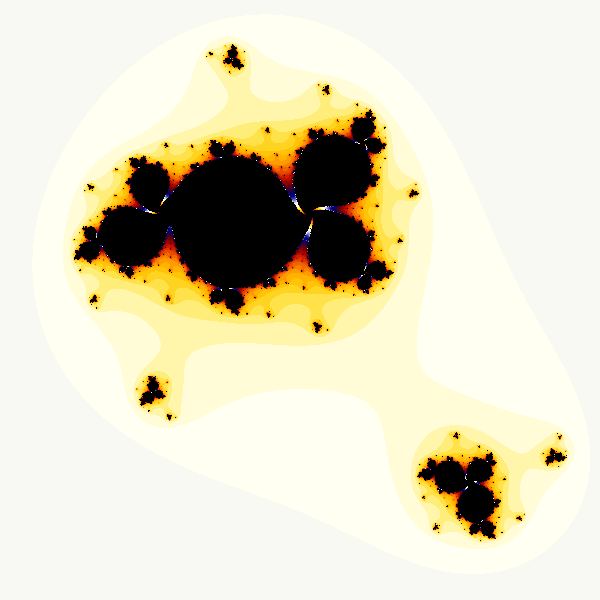
If k = 0+0i, one gets a degenerate Mk with fourfold symmetry; this is the default Cubic Mandelbrot set that I have as the MandelCubicBasic parameter. This fractal is well-known, but most fractal explorers neglect all the other---much more interesting---Mk.

MandelCubicBasic
A small change in the K parameter makes it more interesting.

MandelCubicStack
You can see a lot of cubic Mandelbrots and Julias as follows. Load the rvr.upr parameter file, and click on the different fractals saved in this file. Once you've opened a cubic Mandelbrot or, for that matter, the Rudy set, you can press F7 to see an additional window that shows a cubic Julia correpsonding to the cursor position. If you click, that fractal gets its own window.
Once you've loaded a cubic Mandelbrot Mk, or a cubic Julia Jkc, you can adjust the number values of the Mk and Jkc fractals' Kparam and of the Jkc Cparam in the Window|Tool Window|Layer Properties|Formula window.
Ultra Fractal gives you another way to quickly look at the range of possible Mk sets. Load one of them,and then go to the Formula sheet of the Layer Properties window and click inside one the two K param boxes. When you do this, you'll see a kind of cross-hairs symbol. Click on that, and the Exploring window pops up. You may need to zoom in or out to get a better view.
As you move your cursor around in the Exploring window, you'll see preview images of the various Mk in a FractalMode window. And if you click, that fractal fills the screen.

Detail of MandelCubicInvasionOfTheHrull
If |k| is large (about one or two), one gets an empty Mk. As I mentioned above, all the Mk have symmetry around the origin, meaning that if c = u + iv is in Mk, -c = -u - iv will be in Mk, too.

Detail of MandelCubicPacMan
The appearance of the Mk can be quite interesting. One often sees small replicas of the quadratic Mandelbrot set, though sometimes with wedges cut out of it. By slightly varying a and/or b, once can look at k-sections near each other, and try to visualize stacking them one atop the other.Looking at successive sections, one often gets the impression of the Mk being like a cross-section of a three-dimensional Mandelbrot shape, with buds all over it. But of course the full CCM is four-dimensional, and this shows up in the fact that many of the bud cross-sections have pieces missing from them. Presumably these missing pieces have inappropriate four-dimensional coordinates for intersecting Mk.
As an aid to mathematical visualization, I think of it this way. The CCM is like a three dimensional solid which is free to move pieces of itself to arbitrary time locations. Thus if a section of a bud seems to have the right half missing, we might think of the left half of the bud as being in Monday and the right half of the bud as being in Tuesday, with your cross-section being computed at the Monday time coordinate. I use time not at all in a physical sense here, but simply for the vividness of the image.
Some of the Mk details are fairly amazing.

Detail of MandelCubicZipper
Code alert: I'll now I explain how we compute Mk. The computation is done by fixing k = a + ib and then varying c = x + iy and checking whetherk--fkc-->FINITE, and -k--fkc-->FINITE. On the basis of what I learn while doing this checking, I will assign an Mk color(c) to the pixel representing c. Before starting, I select a BOUND (usualy 4.0) and a value of MAXITERATION (maybe 5,000), and say that k--fkc-->FINITE if for all n less than MAXITERATION, the nth image of k is has norm less than BOUND. As before, we take BOUND to be the square root of seven, and MAXITERATION can be set by the user.
Assuming k = a + ib has been set, our computation of the Mk color(c) for a fixed c = u + iv takes place as follows (this pseudocode description is not fully optimized):
initialize:
iteration = 0;
x = a;
ty = b;
a3 = -3 * ( a * a - b * b );
b3 = -3 * ( 2 * a * b );and then iterate:
{ x2 = tx * tx;
y2 = ty * ty;
xa = x2 - y2 + a3;
yb = 2*tx*ty + b3;
temp = xa * tx - yb * ty + u;
ty = xa * ty + yb * tx + v;
tx = temp;
iteration = iteration + 1;}
until x2 + y2 > BOUND or iteration = MAXITERATION, saving iteration as iteration1;and then reinitialize:
iteration = 0;
tx = -a;
ty = -b;
a3 = -3 * ( a * a - b * b );
b3 = -3 * ( 2 * a * b );and iterate the same computation...
until x2 + y2 > BOUND or iteration = MAXITERATION, saving iteration as iteration2;If iteration1 and iteration2 both equal MAXITERATION, then
Mk color(c) = 0.
Otherwise, Mk color(c) = min(iteration1,iteration2).
As well as the cubic Mk CCM cross-sections, we can also compute
Mc = { k : Jkc is connected};
= { k : ( k--fkc-->FINITE ) AND ( -k--fkc-->FINITE ) }.
The Mc are, to my eye, not as interesting as the Mk. But you can look at them and decide for yourself. Here's one that has a certain gruff charm.

Detail of MandelCubic(Cplane)Ogre
An apparently new fractal which I have enjoyed investigating is this.
R = {k : k is in Mk}
= {k : Jkk is connected}
= {k : ( k --fkk--> FINITE ) AND ( -k
--fkk--> FINITE) }.
I immodestly call it the Rudy set! As I say, I first discovered it some twenty years ago, but computers were pretty slow back then. In the last few days, using Ultra Fractal, I’ve seen much more detail of the Rudy set than ever before. Images that used to take hours to render can pop up in seconds.
Note that the Rudy Set has an absolute or non-relative quality, in that it avoids the choice between the Mk and Mc Mandelbrot Cubics, each of which are a certain kind of orientation-dependent cross-sections of the Cubic Connectedness Map. By going down the Jkk in the definition of the Rudy Set, we reach down to something that’s not relative to any specific orientation. Note also that we could equivalently define the Rudy Set as {c : c is in Mc}. For this is just {c : Jcc is connected}, which is the same as {k : Jkk is connected}.

The Rudy Set
Compare the definition of R as { k : k is in Mk } to the definition of M as { c : c is in Jc }. R is an object which is extremely rich in unusual fractal structures. One good region is the plume between 2 and 3 o'clock. I call this area "Mars".

RudyMars
An image like a rocking horse is found in the Mars region of the Rudy set. This is one of my favorite new spots.

RudyHorse
Another good region is the spike at the top, at 12 o'clock. There is an interesting structure there that is a bit like a Mandelbrot set, but considerably gnarlier. I call it FatBud. This is a great region as well.

RudyFatBud
The Julia sets from inside the Fat Bud zone are lovely and spidery---branching patterns of connected lines.

JuliaCubicFromRudyFatBud
A variation on the Rudy set is ZeroInMk= {k : (0, 0) is in Mk}. This set isn't very interesting. Note that it is not the same as the not-readily-computable MkConnected = {k: Mk is connected}. The thing is, an Mk can contain the origin but still fail to be connected, as in the one shown below.
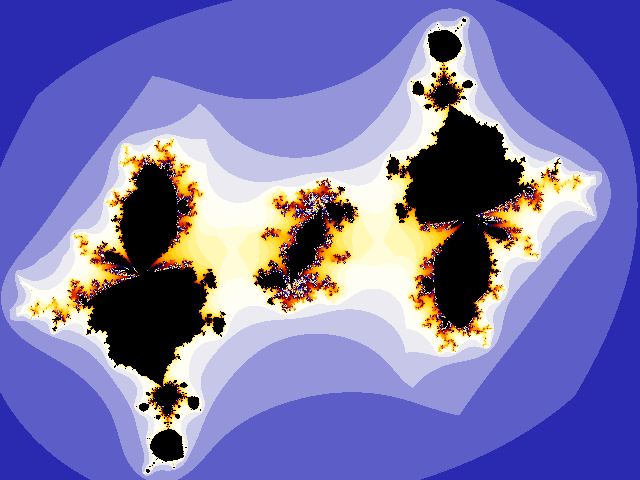
MandelCubicThreePiece.
In any case, because they are defined in terms of Mk instead in terms of Jkk, neither ZeroInMk or MkConnected has the absolute, coordinate-free quality of the Rudy set.
My next step will be to view 3D sets which are stacks of Mk sets that arise as one varies, for instance, the real part of k from -1 to 1. I have a lingering hope that these objects may look bulbous rather than taffy-like, despite the lack of success of some preliminary investigations. See my blog See my blog post on the Mandelbulb for more on this topic.