How
Flies Fly: Kappatau Space Curves
by Rudy Rucker
Department of Mathematics and Computer Science,
San Jose State University, San Jose CA 95192
www.rudyrucker.com
Copyright (C) Rudy Rucker 1999
Appeared in David Wolfe & Tom Rodgers, eds., Puzzlers' Tribute: A Feast for the Mind, A.K.Peters, Natick, MA, 2002
It's interesting to watch flies buzz around. They trace
out curves in space that are marvelously three-dimensional. Birds fly along space curves
too, but their airy swoops are not nearly so bent and twisted as are the paths of flies.
Is there a mathematical language for talking about the
shapes of curves in space? Sure there is. Math is the science of form, and mathematicians
are always studying nature for new forms to talk about.
Historically, space curves were first discussed by the
mathematician Alexis-Claude Clairaut in a paper called "Recherche sur les Courbes a
Double Courbure," published in 1731 when Clairaut was eighteen [1]. Clairaut is said
to have been an attractive, engaging man; he was a popular figure in eighteenth-century
Paris society.
In speaking of "double curvature," Clairaut
meant that a path through three-dimensional space can warp itself in two independent ways;
he thought of a curve in terms of its shadow projections onto, say, the floor and a wall.
In discussing the bending of the planar, "shadow" curves, Clairaut drew on
recent work by the incomparable Isaac Newton.
Newton's mathematical curvature measures a curve's
tendency to bend away from being a straight line. The more the curve bends, the greater is
the absolute value of its curvature. From the viewpoint of a point moving along the curve,
the curvature is said to be positive when the curve bends to the left, and negative when
the curve bends to the right. The size of the curvature is determined by the principle
that a circle of radius R should have curvature of 1/R. The smaller the radius, the
greater the curvature. Figure 1 shows some examples of circular arcs.
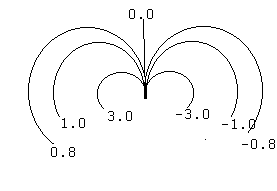
Figure 1: Curvature along circular arcs in the plane.
We often represent a curve in the plane by an equation
involving x and y coordinates. Most calculus students remember a brief, nasty encounter
with Newton's formula for the curvature of a curve; the formula uses fractional powers and
the first and second derivatives of y with respect to x. Fortunately, there is no
necessity for us to trundle out this cruel, ancient idol. Instead we think of curvature as
a primitive notion and express the curve in a more natural way.
The idea is that instead of talking about positions
relative to an arbitrary x axis and y axis, we think of a curve as being a bent
number-line by itself. The curve is marked off in units of "arclength", where
arclength is the distance measured along the curve, just as if the curve were a piece of
rope that you could stretch out next to a ruler.
In this context, the most natural way to describe a plane
curve is by an equation that gives the curvature directly as a function of arclength, an
equation of the form kappa = f(s), where s stands for arclength and kappa is the commonly
used symbol for curvature. Figure 2 shows two famous plane curves which happen to have
simple expressions for curvature as a function of arclength. The catenary curve is the
shape assumed by a chain (or bridge cable) suspended from two points, while the
logarithmic spiral is a form very popular among our friends the molluscs.
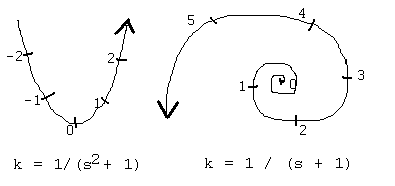
Figure 2: The catenary and the logarithmic spiral
expressed by natural equations, with curvature kappa a function of arclength s.
Note that for the spiral, the center is where s approaches
-1; if you jump over the anomalous central point and push down into larger negative values
of s, you produce a mirror-image of the spiral.
It would be nice to also think of space curves in a
natural, coordinate-free way --- surely this is the way a fly buzzing around in the center
of an empty room must think. Profound mathematical insights come hard, and it was a
hundred and twenty years after Clairaut before the correct way to represent a space curve
by intrinsic natural equations was finally discovered --- by the French mathematicians
Joseph Alfred Serret and Frederic-Jean Frenet.
The idea is that at each point of a space curve one can
define two numerical quantities called curvature and torsion. The curvature of a space
curve is essentially the same as the curvature of a plane curve: it measures how rapidly
the curve is bending to one side. The torsion measures a curve's tendency to twist out of
a plane. But what exactly is meant by "bend to one side," and "twist out of
a plane"? Which plane?
The idea is that at each point P of a space curve you can
define three mutually perpendicular unit-length vectors: the tangent T, the normal N, and
the binormal B. T shows the direction the curve is moving in, N lies along the direction
which the curve is currently bending in, and B is a vector perpendicular to T and N. (In
terms of the vector cross product, T cross N is B, N cross B is T, and B cross T is N.)
For space curves we ordinarily work only with positive values of curvature, and have N
point in the direction in which the curve is actually bending. (In certain of the
analytical curves we’ll look at later we relax this condition and allow negative
curvature of space curves.)
Taken together, T, N and B make up the so-called
"moving trihedron of a space curve". In Figure 3 we show part of a space curve
(actually a helix) with several instances of the moving trihedron. So that it's easier to
see the three-dimensionality of the image, we draw the curve as a ribbon like a twisted
ladder. The curve runs along one edge of the ladder, and the rungs of the ladder
correspond to the directions of successive normals to the curve.
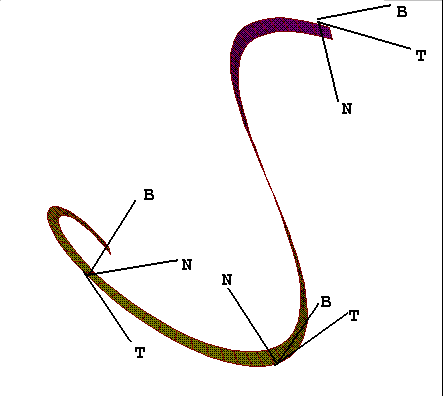
Figure 3: The moving trihedron of a space curve: T the
tangent, N the normal, and B the binormal.
To understand exactly how the normal is defined, it helps
to think of the notion of the "osculating" (kissing) plane. At each point of a
space curve there is some plane that best fits the curve at that point. The tangent vector
T lies in this plane, and the direction perpendicular to T in this plane holds the normal
N. The binormal is a vector perpendicular to the osculating plane.
With the idea of the moving trihedron in mind, we can now
say that the curvature measures the rate at which the tangent turns, and the torsion
measures the rate at which the binormal turns.
Note that T, N and B are always selected so as to form a
right-handed coordinate system. This means that if you hold out the thumb, index finger
and middle finger of your right hand, these directions correspond to the tangent, the
normal, and the binormal.
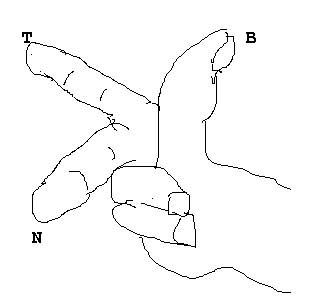
Figure 4: A right-hand as a trihedron.
Just as the circle is the plane curve characterized by
having constant curvature, the helix is the space curve characterized by having constant
curvature and constant torsion. Figure 5 shows how the signs of the curvature and torsion
affect the shapes of plane and space curves.
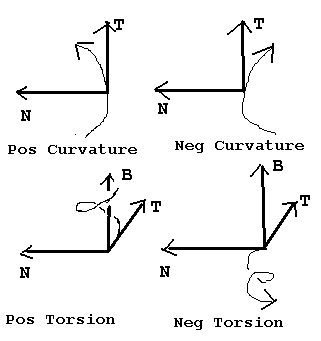
Figure 5: How the signs of the curvature and torsion
affect the motion of a curve.
Now let's look for some space formulae analogous to the
plane formula stating that the curvature of a circle of radius R is 1/R. Think of a helix
as wrapping around a cylinder --- like a vine growing up a post. Let R be the radius of
the cylinder, and let H represent the turn-height: the vertical distance it takes the
helix to make one complete turn (and to make the formulae nicer, we measure turn-height in
units 2*pi as large as the units we measure R in.)
The sizes of the curvature and torsion on a helix with
radius R and turn-height H are given by two nice equations. We write "tau" for
torsion and, as before, "kappa" for curvature:
kappa = R / (R^2 + H^2), and
tau = H / (R^2 + H^2).
It's an interesting exercise in algebra to try and turn
these two equations around and solve for R and H in terms of kappa and tau. (Hint: Start
by computing kappa^2 + tau^2. When you're done, your new equations will look a lot like
the original equations.)
Some initial things to notice are that if H is much
smaller than R, you get a curvature roughly equal to 1/R, just like for a circle, and a
tau very close to 0. If, on the other hand, R is very close to zero, then the torsion is
roughly 1/H while the curvature is close to 0. A fly which does a barrel-roll while moving
through a nearly straight distance of H has a torsion of 1/H. The faster it can roll, the
greater is its torsion.
A less obvious fact is that if we look down on a plane
showing all possible positive combinations R and H, the lines of constant curvature lie on
horizontal semi-circles; while the points representing constant torsion lie on vertical
semi-circles. The curvature and torsion combinations gotten by stretching a given Slinky
lie along a quarter circle centered on the origin. Apparently the two families of
semi-circles are perpendicular to each other.
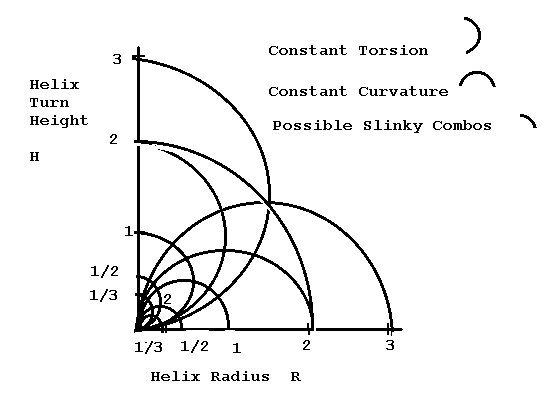
Figure 6: Lines of constant curvature and torsion for
combinations of R and H.
Suppose I have a helix like a steel Slinky spring. What
happens to the curvature and the torsion as I stretch a single turn of it without
untwisting? Suppose that the initial radius of the helix is A. Given the physical fact
that the length of one twist of the Slinky keeps the same length, you can show that as you
stretch it, R^2 + H^2 will stay constant at a value of A^2, which corresponds to a circle
of radius A around the origin of the R-H plane. As you stretch a Slinky loop with the
particular starting radius of 2, its R and H values will move along the dotted blue line
shown in Figure 6. Figure 7 shows what a few of the intermediate positions will look like.
Curvature is being traded off for torsion.
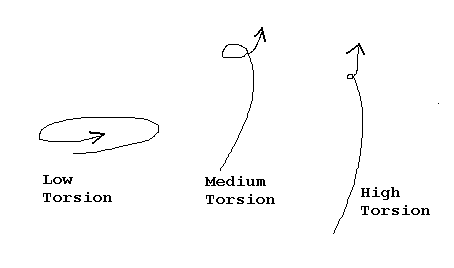
Figure 7: Stretching a Slinky turns curvature into
torsion.
Here's another algebra problem: If you know that R^2 + H^2
= A^2, what can you say about the sum kappa^2 + tau^2?
One fact that seems odd at first is that the curvature and
torsion of a helix are dependent on the size of the helix. If you make both R and H five
times as big, you make the torsion and curvature 1/10 as big. If you make R and H N times
as big, you make the curvature and torsion 1/(2*N) as big.
But this makes sense if you think of a fly that switches
from a small helix to a big helix; it is indeed changing the way that its flying, so it
makes sense that the kappa and the tau should change.

Figure 8: Changing Curvature and Torsion.
This observation suggests a simple way to express the
difference between flies and birds --- flies fly with much higher curvature and torsion
than do the birds. Gnats, for that matter, fly even more tightly knotted paths, and have
very large values of curvature and torsion.
Just as in the plane, a space curve can be specified in
terms of natural equations that give the curvature and torsion as functions of the
arclength. These equations have the form kappa = f(s) and tau = g(s). The shape and size
of the space curve is uniquely determined by the curvature and the torsion functions.
Figures 9 and 10 shows two intriguing space curves given by simple curvature and torsion
functions.
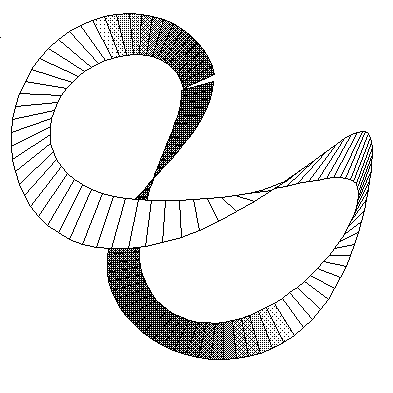
Figure 9: The rocker, with natural equations kappa = 1
and tau = sine(arclength)

Figure 10: The phone-cord, with natural equations kappa =
sine(arclength) and tau = 1.
Well, actually I used kappa = 10*sine(arclength) and tau =
3 to make the picture look better. Note that this is a space curve where we do allow
ourselves to put in negative values for the curvature.
There is not a large literature on these
"kappatau" curves, so I've given my own names to these two: the rocker, and the
phone-cord.
At one time I thought that the rocker was a correct way to
represent the seam on a tennis-ball or the stitching on a baseball, but helpful email from
the great mathematician John Horton Conway convinced me I was wrong. Conway makes the
anthropological conjecture that every time a mathematician discovers a curve that he or
she thinks might be the true baseball curve, the curve is a different one.
An analysis of the real-world baseball stitch curve can be
found in the web-published paper "Designing A Baseball Cover by Richard Thompson of
the Department of Mathematics, University of Arizona [2]. It turns out the baseball stitch
curve is based on something so prosaic as a patented 1860s pen and ink drawing of a plane
shape used to cut out the leather for a half of a baseball, a shape arrived at by trial
and error. Thompson finds a fairly gnarly closed-form approximation of this shape.
Not only does my rocker fail to match the baseball stitch
curve, it can be proved that the rocker curve does not in fact lie on the surface of a
sphere (even though it kind of looks like it does). It fails to satisfy the following
necessary condition for lying on the surface of the sphere, where s stands for arclength
(see [3]).
d/ds[(1/tau)*d/ds(1/kappa)] + tau*(1/kappa) = 0
(For kappa = 1 and tau = sin(s), the left-hand side of
this is sin(s), which isn’t 0.)
Numerical estimates indicate that the arclength of the
rocker has exactly twice the length of a circle of the same radius. This suggests an easy
way to make a rocker. Cut out two identical annuli (thick circles) from some fairly stiff
paper (manila file folders are good), cut radial slits in the annuli, tape two of the
slit-edges together, bend the annuli in two different ways (one like a clockwise helix and
one like a counterclockwise helix) and tape the other two slit-edges together, forming a
continuous band of double length . Because an annulus cannot bend along its osculating
plane, the curvature of the shape is fixed along the arclength. Because half the band is
like a clockwise helix and half is like a counterclockwise helix, when the shape relaxes,
the torsion presumably varies with the arclength like a sine wave function that goes
between plus one and minus one. The torsion seems to be zero at the two places where the
slits are taped together. Note that I have not proved that my empirical paper rocker is
the same as my mathematical rocker, this is simply my conjecture.
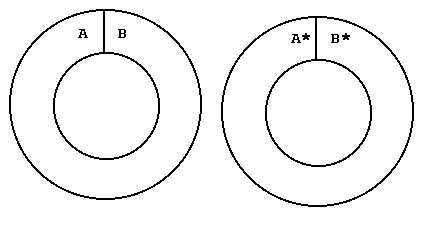
Figure 11: Make your own rocker.
- To make the rocker, make a (larger) copy of Figure 11 on
stiff paper.
- Cut along all solid lines.
- Tape edge A to edge B* with the letters on the same side.
- Bend the two rings in the opposite sense.
- Tape edge A* to edge B with the letters on the same side.
How were the images in Figures 9 and 10 generated? They
use an algorithm based on the 1851 formulae of Serret and Frenet. (See, for instance,
Struik's classic work [4] for details; note that this book is now available as an
inexpensive Dover paperback reprint.) Let's state the formulae in "differential"
form. The question the formulae address is this: when we do a small displacement ds along
a space curve, what is the displacement dT, dN, and dB of the vectors in the moving
trihedron?
dT =( kappa*N )*ds
dN =( - kappa*T + tau*B )*ds
dB =( - tau*N )*ds
The first and third equations correspond, respectively, to
the definitions of curvature and torsion. The second equation describes the
"back-reaction" of the T and B motions on N.
Since we are lucky enough to live in three-dimensional
space, it is possible for us to experiment with our bodies and to perceive directly why
the Serret-Frenet formulae are true. To experience the equations, you should, if possible,
stick out your right hand's thumb, index finger, and middle finger as shown in Figure 4.
Now start trying to "fly" your trihedron around according to these rules: (1)
The index finger always points in the direction your hand is moving. (2) You are allowed
to turn the index finger towards or away from direction of the middle finger by a motion
corresponding to rotating around the axis of your thumb. (3) You are allowed to turn the
thumb towards or away from the middle finger by a motion corresponding to rotating around
the axis of your forefinger.
To get clear on what's meant by motion (2), grab your
thumb with you left hand and make as if you were trying to unscrew it from your hand. This
is a kind of "yawing" motion, and it corresponds to the first of the three
Serret-Frenet formulae: the change in the tangent is equal to the curvature times normal.
Motion (3) corresponds to grabbing your index finger with your left hand and trying to
unscrew that finger. This is a kind of "rolling" motion, and it corresponds to
the third of the Serret-Frenet formulae: the change in the binormal is the negative of the
torsion times the normal.
In thinking of flying along a space curve you should
explicitly resist thinking about boats and airplanes which have a built-in visual
trihedron which generally does not correspond to the moving trihedron of the space curve.
If you do want to think about a machine, imagine a rocket which never slows down and never
speeds up, which can turn left or right --- relative to you the passenger --- and which
can roll. Or better yet, think about being a cybernetic house-fly.
An exciting thing about the Frenet-Serret formulae is that
they lend themselves quite directly to creating a numerical computer simulation to create
kappatau space curves with arbitrary curvature and torsion. To write the code in readable
form, we create a Vector3 class with a few handy methods and overloaded operators. The
heart of the algorithm's main loop looks about like this:
P = P + ds * T; //operator*(Real, Vector3) is overloaded
to mean scalar product.
s = s + ds;
T = T + (kappa(s) * ds) * N; //Bend. + is overloaded to
mean vector addition.
B = B + ( -tau(s) * ds) * N; //Twist.
T.Normalize(); //The Vector3::Normalize() method makes T
have unit length.
B.Normalize(); //Makes B have unit length.
N = (B * T); //operator*(Vector3, Vector3) is overloaded
to mean cross product.
As far as I know, very little mathematical work has been
done with kappatau curves because in the past nobody could visualize them. I first
implemented the algorithm as a Mathematica notebook for the Macintosh and for Windows
machines, and then I wrote a stand-alone Windows program called Kaptau. You can download
either of the Mathematica notebooks or the stand-alone Windows program from a page on my
web-site [5].
Coming back to this paper's first two paragraphs, what can
a mathematician say about the way flies fly? I think that flies generally move along at a
constant speed, as if tracing a space curve parameterized by its arclength, and that they
manage to loiter here and speed away from there by varying their curvature and torsion
between low and high values.
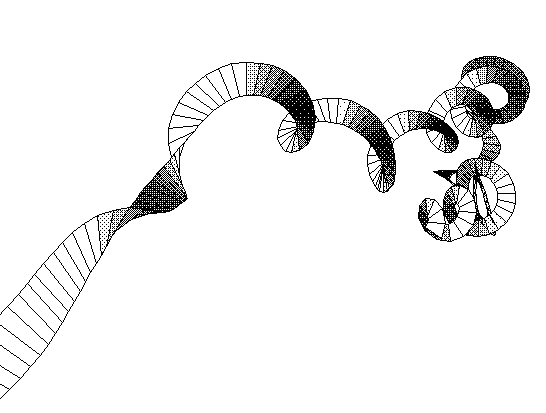
Figure 12: A kappatau curve with curvature varying as a
random walk.
References:
- Morris Kline, Mathematical Thought From Ancient To Modern
Times, Oxford U. Press, New York, 1972, p. 557.
- Richard Thompson, "Designing a Baseball Cover,"
at http://www.mathsoft.com/asolve/baseball/baseball.html,
1996.
- Yung-Chow Wong, "On An Explicit Characterization of
Spherical Curves," Proceedings of the American Mathematical Society 34 (July, 1972),
pp. 239-242.
- Dirk J. Struik, Lectures on Classical Differential
Geometry, Addison-Wesley, Reading, Mass, 1961.
- Rudy Rucker, "Kappa Tau Curves Download Page," at
http://www.rudyrucker.com/oldhomepage/kappatau.htm,
first posted 1997.
|