These days there are a wide range of competing notions about the size and shape of the space that we live in. The cosmologists are kind of lost. So I might as well put in my two cents worth!

I’ll group my comments in three sections, relating to how big space is. 1: Finite, 2: Potentially Infinite, and 3: Actually Infinite.

This initial post is somewhat hasty, and I may refine it a bit more in the days to come.

[1: Finite Space] Space is finite, but without edges. Although the total volume of space is expanding, it won’t expand forever.

There are different ways in which space can be finite without edges. You can have a so-called flat 3D torus, in which you essentially take a cubical room and glue the opposite walls together in pairs, and glue the ceiling to the floor. I don’t mean that you crush the walls in. I mean that you pull them around and stretch—think of taking a square of paper and gluing two opposite edges to make a cylinder, and then gluing the cylinder’s two ends together to make a torus. By the way you’d need to be in 4D space to smoothly make the 3D torus.

Another very well known finite 3D space is the hypersurface of a hypersphere, a 3D space analogous to the surface of a sphere. Or space might be lumpy as in the picture below, with regions of various curvature.

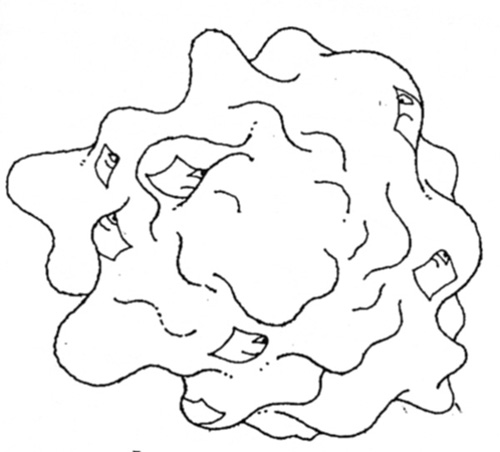
[Illustration by David Povilaitis from my book, The Fourth Dimension]

This picture shows our two-dimensional Flatland friend A Square on the surface of a finite space. A standard move in trying to visualize curved 3D space is to think of a flat guy living on a curved 2D space.

But people often think our space ought to be smooth. If you want a smooth space that’s not sphere-like you can look at an odd-ball finite space known as Poincare dodecahedral space, which can be produced by gluing together opposite faces of a dodecahedron with the smallest amount of clockwise twist needed to make the pentagons match.

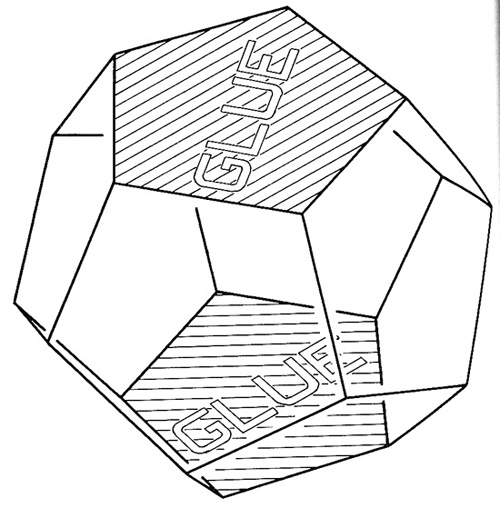
I copied this picture from a wonderful and easily-read book by Jeffrey R. Weeks, The Shape of Space, now out in a new edition. In the early 1980s, I used to correspond with Weeks about the fourth dimension, and I’m proud to say that I suggested the title for his book. More recently, Weeks published an interesting paper discussing the notion that our universe’s space might actually be Poincare dodecahedral space. Weeks also has some nice geometry visualization software on line.

Although this is far from being obvious, you can also produce the Poincare dodecahedral space by taking two pretzels, that is two two-holed donuts, and gluing their surfaces together—analogously to how you might produce a hypersphere by gluing the surfaces of two spheres together. Of course for these weird gluings to work and for everything to look smooth, you’d have to warp the hell out of the pieces in a higher-dimensional space, but mathematicians don’t mind that kind of thing.

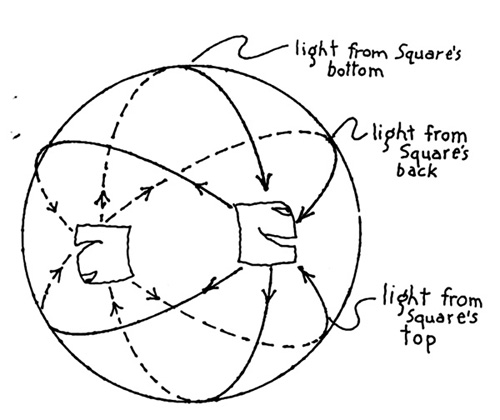
[Another Povilaitis illo from my book, The Fourth Dimension.]

How would you decide what the shape of our space is, anyway? It has to do with cosmic background radiation (CBR), the faint hiss of microwave static in the sky, and the possibility that we might be able to see “around” our space in certain directions. Disappointingly, the very latest measurements on the CBR suggest that, if space is finite, it’s just as likely to be a mere hypersphere as being a Poincare dodecahedral space. Although it might not be finite at all, as I’ll discuss below.

The reason I’m into this topic these days is because I just read a very good book by Donal O’Shea, The Poincare Conjecture, involving an eccentric (are there any other kind?) mathematician, Grigory Perelman, who proved old-time mathematician Henri Poincare’s conjecture that, um, well, that something that acts enough like a hypersphere really is a hypersphere.

By the way, the Poincare dodecahedral space is different enough (what with those hyper pretzel holes) that it doesn’t “act like a hypersphere” in the sesne that we’re talking about. But—until Perelman proved the Poincare conjecture (around 2002)—there was a lingering chance that there might be something that does act very much like a hypersphere that isn’t a hypersphere.

Perelman might get $1,000,000 from the Clay Mathematics Institute for his proof. But he’s not saying yet if he would accept the prize. He has some issues with the mathematics community.

[2: Potentially Infinite Space] Space is finite without edges, and it will expand forever, eventually passing through each finite size.

It’s well known that space is expanding, that is, all the galaxies are rushing apart from each other. Twenty years ago, people thought that space had no intrinsic reason to expand forever and that even though it was now expanding, the gravitational attraction of the galaxies would eventually pull it back. In this context, the Flatland image to use is that of an expanding balloon.

But now we’ve got this “dark energy” factor that may make our universe expand forever. Nobody really knows what dark energy is .

Some careless speakers say this means that an endless expansion means that our space is infinite, but that’s not the kind of infinity that I’m after. I want infinity here right now.

[3: Actually Infinite Space] Space is infinite right now, like an endless Euclidean 3D space.

How does infinite space jibe with the “Big Bang,” which is often thought of in terms of space expanding from a point?

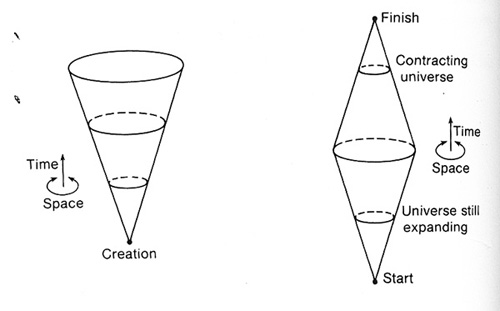
[Figure from my first book, Geometry, Relativity and the Fourth Dimension. The left image represents a hyperspherical space that expands from a point-like Big Bang; the right image extends this to a scenario where space collapses back to a point.]

The way out is the so-called “ekpyrotic scenario” or “cyclic universe” which seems compatible with space being infinite and still having a “big bang” sort of event. The idea, as I understand it, is that we think of two endless parallel universes, two infinite hypersheets or “branes” of space. They’re quite close, perhaps only a few million Planck lengths apart.

The the branes are oscillating back and forth and that every few billion years they bounce off one another, and in these wonderful bounce instants — ZOW! — every crevice of space is flooded with a burst of energy. And the energy turns into matter, and it’s all rushing apart. See Princeton physicist Paul Steinhardt’s site for some short papers about it, an animation, and a link to his The Endless Universe , a book about the cyclic universe, written with Neil Turok. Rather than talking about the Big Bang, they talk about the Big Splat! Here’s a five minute talk by Steinhardt with some graphic animations:

[YouTube talk by Steinhardt]

By the way, you might think that an infinite space wouldn’t have room to be expanding, but simply think of a space in which every minute you map the point (x,y, z) into (2x, 2y, 2z). Contrary to one’s initial intuition, the expansion in such a space is homogeneous and the origin won’t look special. Wherever you are, you’re pulling away of stuff behind you and the stuff ahead is pulling ahead of you.

Really, you don’t have to think of the space itself expanding in the cyclic universe scenario, you can just think of the matter rushing apart. And eventually it’s all so far apart that the universes are quite cool and empty. And then they drift back together for another Great Spacef*ck and — ZOW again.

The notion of a cosmos in which we have two parallel branes of reality is something I adapted from the physicist Lisa Randall, for my last novel, Postsingular, where I call the two parallel worlds the Lobrane and the Hibrane. This carries over into the sequel Hylozoic, too.

In a quick web search, I do see some ill-informed people arguing against infinite universes on a priori reasons. These are rehashes of pre-Cantorian Scholastic arguments that are derived from the mistaken notion that an actual infinite is inherently contradictory.

I’ve always meant to write an SF story about an infinite Flat Earth. Where you could walk or drive and if you went far enough you’d get somewhere that nobody in your home civilization had ever been. Like an Age of Exploration that never has to stop.

One of my favorite papers about infinite universes is by Max Tegmark. In his paper, “Parallel Universes,” he argues that instead of worrying about having alternate worlds, we can just suppose that our universe goes on forever in space right now.

Eventually, I’m going to be talking about 4: Transfinite Space, but this blog post is too small, and my energy too low, to present all that today. Quite briefly, the third of my psipunk Postsingular books will (probably) be called Transfinite, and will involve some adventures in a world where actual infinities exist—as in my early novel White Light. But this time I’ll do it a little differently, I want the infinities to leak back into our actual lives.

In an earlier blog post I mentioned that I was warming up for writing Transfinite by writing a story about infinity that ended up with the title “Jack and the Aktuals.” If all goes well, this story will appear in the new online fiction site, Tor.com this summer.

Maybe if I could get out to transfinite space, I’d find my missing mathematician friend Jim Carrig there, safe in heaven dead.

By the way, I found an online reference to a painter, Alfred Russell, who started out as an abstract expressionist, and later turned to classical style.

He did a painting called “Transfinite Space” around 1950.

And another called “Transfinite Structure” around 1951. I’m thinking maybe there’s lots of much smaller quadrilaterals that we don’t see!

I also see that there’s an anthology of SF stories by A. E. van Vogt called Transfinite.

This entry was posted on Sunday, April 20th, 2008 at 4:57 pm and is filed under Rudy's Blog. You can follow any responses to this entry through the RSS 2.0 feed. Both comments and pings are currently closed.